Boule unité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
tony800
- Membre Relatif
- Messages: 134
- Enregistré le: 18 Mar 2006, 16:20
-
 par tony800 » 20 Nov 2008, 15:30
par tony800 » 20 Nov 2008, 15:30
Bonjour,
J'aurais besoin de déterminer la boule :
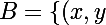 \in \mathb{R^2} | N (x,y) \leq 1\}})
avec
 = \int^1_0 |x + \sqrt{2}ty|dt})
La valeur absolue me bloque, je ne vois pas comment m'en débarasser.
Pourriez-vous me donner un coup de main?
Merci d'avance
Au revoir
-
tony800
- Membre Relatif
- Messages: 134
- Enregistré le: 18 Mar 2006, 16:20
-
 par tony800 » 20 Nov 2008, 15:49
par tony800 » 20 Nov 2008, 15:49
Dans ce cas il faut que je le fasse en fonction de t?
Ce qui donnerait :
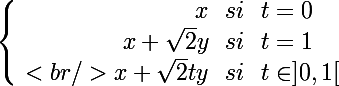
Et je détaillerais chaque cas?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 20 Nov 2008, 16:04
par Doraki » 20 Nov 2008, 16:04
Il faudrait peut-être que les cas que tu considères aient un rapport avec le signe de l'expression sous la valeur absolue, tu crois pas ?
Il peut se passer 3 trucs selon les valeurs de x et y :
Ou bien l'expression est toujours positive et l'intégrale se calcule facilement,
ou bien elle est toujours négative et elle se calcule encore facilement,
ou bien elle change de signe pour un t dans [0;1] et il faut donc séparer l'intégrale en deux, et là sa se calcule facilement.
-
tony800
- Membre Relatif
- Messages: 134
- Enregistré le: 18 Mar 2006, 16:20
-
 par tony800 » 20 Nov 2008, 16:47
par tony800 » 20 Nov 2008, 16:47
Non, je n'ai pas fait de dessin, je ne vois pas comment le faire d'ailleurs.
On a \forall t \in [0,1] -1\leq x+\sqrt {2}ty\leq1
Sinon pour les 3 cas j'aurais donc :
1/

si

2/

si

3/

si
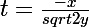
L'intégrale donnerait donc :
1/

2/
x^2}{4\sqrt{2}y})
3/
x^2}{4\sqrt{2}y})
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 20 Nov 2008, 17:06
par Doraki » 20 Nov 2008, 17:06
tony800 a écrit:On a

hein ? quoi ?
C'est vrai.
3/

si
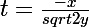
Ca veut rien dire.
L'intégrale donnerait donc :
1/

2/
x^2}{4\sqrt{2}y})
3/
x^2}{4\sqrt{2}y})
Serais-tu en train de dire un truc du genre "dans le cas 1, c'est à dire pour

, alors N(x,y) =

?
Si c'est le cas, ben ça veut rien dire parceque la condition sur (x,y) parle d'un t qui n'existe pas.
Dans quelles condition sur (x,y) est-ce que l'expression intégrée reste positive pour tout t dans l'intervalle d'intégration [0,1] ? Que vaut N(x,y) dans ce cas là ?
-
tony800
- Membre Relatif
- Messages: 134
- Enregistré le: 18 Mar 2006, 16:20
-
 par tony800 » 20 Nov 2008, 17:16
par tony800 » 20 Nov 2008, 17:16
Dans ce cas il faut que je calcul l'intégrale est seulement ensuite je formule mes conditions?
-
tony800
- Membre Relatif
- Messages: 134
- Enregistré le: 18 Mar 2006, 16:20
-
 par tony800 » 20 Nov 2008, 17:57
par tony800 » 20 Nov 2008, 17:57
Pour fixer x et y : je définis par exemple x = t, et j'en déduis y.
Mais je ne vous pas la paramètrisation que je dois faire, j'ai essayé avec y =tx, x = ty, x = t, y = t, mais je n'ai rien trouvé de facile à exploiter.
-
tony800
- Membre Relatif
- Messages: 134
- Enregistré le: 18 Mar 2006, 16:20
-
 par tony800 » 20 Nov 2008, 18:35
par tony800 » 20 Nov 2008, 18:35
Doit-on fixer x et y entre [-1,1]?
Les 3 cas sont :
1/

2/

3/
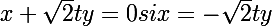
Mais je ne vois pas comment faire la suite.
Doit-on calculer l'intégrale dans chaque cas?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 20 Nov 2008, 19:14
par Doraki » 20 Nov 2008, 19:14
tu peux calculer, au hasard, N(2,3), N(-1,2) et N(-5,2) ?
-
tony800
- Membre Relatif
- Messages: 134
- Enregistré le: 18 Mar 2006, 16:20
-
 par tony800 » 20 Nov 2008, 20:19
par tony800 » 20 Nov 2008, 20:19
Je viens d'effectuer les calculs, et j'ai remarqué qu'on avait bien 3 cas différents, mais je ne vois pas comment le généraliser avec x et y.
Enfin surtout comment je peux en déduire la boule unité.
-
seriousme
- Membre Relatif
- Messages: 122
- Enregistré le: 26 Fév 2007, 13:10
-
 par seriousme » 20 Nov 2008, 21:38
par seriousme » 20 Nov 2008, 21:38
Avec un changement de variable et un réarrangement c'est plus évident :
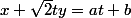
Avec

et
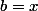
L'expression est une fonction affine de t : au pire il y a quatre cas à distinguer.
Mais comme l'intervalle d'étude est [0, 1] les cas
 \in {\mathbb{R}^+}^2)
et
 \in {\mathbb{R}^-}^2)
sont simples et permettent de retirer la valeur absolue.
-
tony800
- Membre Relatif
- Messages: 134
- Enregistré le: 18 Mar 2006, 16:20
-
 par tony800 » 21 Nov 2008, 17:39
par tony800 » 21 Nov 2008, 17:39
Merci bien pour votre aide.
Maintenant, cela me parait très clair.
J'avais continué cet exercice et j'avais commencé à trouver quelques trucs.
-
tony800
- Membre Relatif
- Messages: 134
- Enregistré le: 18 Mar 2006, 16:20
-
 par tony800 » 24 Nov 2008, 21:51
par tony800 » 24 Nov 2008, 21:51
J'ai dit que je venais de comprendre, c'est vrai, mais j'ai un souci pour les 2 autres cas.
J'ai fait le cas ou a
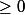
et
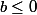
et je dois décomposer l'intégrale.
J'ai dit que l'intégrale connair :
yt dt))
mais je pense que c'est faux.
Et les mêmes calculs pour le cas ou a \leq 0 et b \geq 0, avec les signes opposés.
Pourriez-vous me donnez un conseil en plus?
-
tony800
- Membre Relatif
- Messages: 134
- Enregistré le: 18 Mar 2006, 16:20
-
 par tony800 » 25 Nov 2008, 19:14
par tony800 » 25 Nov 2008, 19:14
Personne pour me dire si ce que j'ai fait était juste?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
si
si
si