Equation diophantienne
Olympiades mathématiques, énigmes et défis
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 24 Nov 2008, 21:01
par lapras » 24 Nov 2008, 21:01
Bonsoir,
résoudre
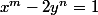
pour


tels que il existe
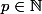
tel que

est premier et
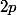
divise

et

divise

.
PS : l'exercice en soit n'est pas difficile, je poste juste parce que le résultat est interessant !
-
Asymetric
- Messages: 6
- Enregistré le: 15 Nov 2008, 00:02
-
 par Asymetric » 24 Nov 2008, 21:05
par Asymetric » 24 Nov 2008, 21:05
Equation de Pell ?
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 24 Nov 2008, 21:06
par lapras » 24 Nov 2008, 21:06
Je ne les ai pas utilisées... Il ne faut pas toujours se référer aux classiques d'olympiades ! (Pell est beaucoup utilisé).
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 24 Nov 2008, 21:31
par ThSQ » 24 Nov 2008, 21:31
Pell c'est plutôt avec des carrés :k2k:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 24 Nov 2008, 21:36
par Zweig » 24 Nov 2008, 21:36
Détrompe-toi, une variante de Pell est

, il y'a aussi de la théorie autour de
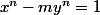
Voir l'ouvrage "Pell's equation" de Barbeau.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 24 Nov 2008, 21:37
par Zweig » 24 Nov 2008, 21:37
Détrompe-toi, une variante de Pell est

, il y'a aussi de la théorie autour de

Voir l'ouvrage "Pell's equation" de Barbeau.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 24 Nov 2008, 21:43
par lapras » 24 Nov 2008, 21:43
Oula je vois mal comment ils généralisent à des exposants quelconques... Déja que le cas 3 est bien sympa ! :doh:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 26 Nov 2008, 19:38
par lapras » 26 Nov 2008, 19:38
Alors quelqun a trouvé ? :happy2:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 27 Nov 2008, 19:02
par lapras » 27 Nov 2008, 19:02
Voici ma solution :
On étudie l'équation

donc
(x^p+1) = 2y^p)
or
 = 2)
On a dans un premier cas :
^p)
les deux facteurs de droite sont premiers entres eux,
Il existe donc a entier tel que
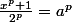
donc
^p = 1)
ce qui est clairement impossible sauf si x = 1 et a = 0 ce qui fournit la solution
 = (1,0))
(factorisation)
deuxieme cas :
^p)
donc
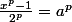
donc
^p - x^p = 1)
ce qui est impossible
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités