Espace vectoriel

[selma123]

bonsoir
ptite question
comment on peut trouver une base du sous-espace vectoriel de
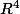
suivant:
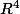
F={(x,y,z,t) |x+y+z+t=0}

merci d'avance

[nuage]

Salut,
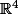
on cherche 3 vecteurs indépendants de tels que
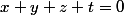
Par exemple
etc...

[selma123]

Salut,
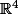
on cherche 3 vecteurs indépendants de tels que
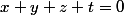
Par exemple
etc...

merci :++:

[leon1789]

oui, prendre 3 vecteurs "au hasard" dans F , mais les plus simples possibles (pas nuls quand même :happy2: ) pour démontrer facilement qu'ils sont bien libres

[seriousme]

Voici une méthode simple :
- exprimer la forme générale d'un vecteur de cet espace :

- exprimer ce vecteur comme combinaison linéaire de x, y et z :

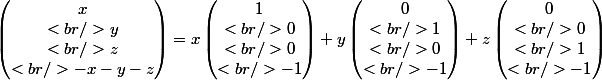
- en déduire une base :

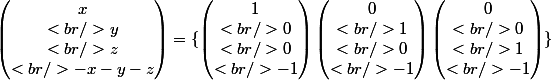
Par construction la famille de ces vecteurs est en effet forcément libre et génératrice.

[selma123]

merci bcp pour votre reponse :++: :++:

[selma123]

bonsoir
svp quelqu'un peut m'expliquer c'est quoi une application endomorphisme
car j'ai un exercice d'espace vectoriel et on me demande si cettes2 applications de dans est endomorphisme de (,+,.)
f_1: (,)-----> (1+,)
f_2:(,)---->(sin(),)
merci d'avance