Problèmes - ensemble ?

[alexisdelouhans]

Bonjour, je suis en 1ère S et mon professeur m'a donné un devoir à la maison. J'ai réussi les 2 premiers exercices mais je bloque sur le troisième et les deux premières questions.

Le voici:

F désigne l'ensemble des fonctions numériques dont l'ensemble de définition est R (réel), I et P sont les sous-ensembles de F constitués respectivement des fonctions impaires et paires.

Questions:

1. Démontrer que les ensembles F, I et P sont stables par combinaisons linéaire*.

Le professeur nous a mis:

*[ On sait qu'un ensemble E (muni d'une multiplication par un réel et d'une addition) est dit stable par combinaisons linéaires lorsque pour tout réel alpha & béta et pour tous éléments, f et g de E: (alpha x + béta g) appartient à E. ]

2. Démontrer que pour tout élément, f, de F il existe un unique élément, (p,i), de P X(fois) I tel que: f= p + i.

---------

Pouvez-vous m'aider s'il vous plaît, je vous en serai reconnaissant.
Merci.

[Luc]

Salut,

Pour la 1., il faut utiliser la définition d'une combinaison linéaire:

Une combinaison linéaire de et c'est , avec 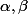des réels.

Il faut montrer que si f et g sont deux fonctions, toute combinaison linéaire de f et g est encore une fonction.

Que si f et g sont deux fonctions paire, toute combinaison linéaire de f et g est encore une fonction paire.

Que si f et g sont deux fonctions impaire, toute combinaison linéaire de f et g est enconre une fonction impaire.

2. Pense à f(-x).

PS: Des ensembles stables par combinaisons linéaires (et non vides) comme ceux-ci sont appelés des espaces vectoriels sur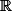

Luc