Bonjour à tous!
Je bloque sur un probleme dont le titre evocateur est:"avis de recherche."
J'esperais que vous pourriez m'éclairer :)
Voici le probleme :
Déterminer trois réels a,b,c tels que la courbe d'équation y=ax+b+c/(x-1) passe par A(3;2) ,admette en ce point une tangente horizontale e possède au point d'abcisse 2 une tangente parallèle à la droite d'équation y=3x+2
Un probleme bref, mais qui cache bien des difficultés pour moi..
MErci d'avance !!
Petit probleme de Dérivés!
8 messages
- Page 1 sur 1
Salut,
Il faut bien lire l'énoncé et le traduire en équations.
la courbe d'équation y=ax+b+c/(x-1) passe par A(3;2): une équation
admette en ce point une tangente horizontale: une autre équation
possède au point d'abcisse 2 une tangente parallèle à la droite d'équation y=3x+2: une troisième équation
Deux problèmes indépendants donc:
1) Trouver les trois équations
2) Résoudre le système 3x3 en (a,b,c)
Il ne faut pas oublier que la définition de la dérivée en un point, c'est le coefficient directeur de la tangente en ce point. (c'est très utile ici)
Luc
PS: J'aime bien ta citation!
Il faut bien lire l'énoncé et le traduire en équations.
la courbe d'équation y=ax+b+c/(x-1) passe par A(3;2): une équation
admette en ce point une tangente horizontale: une autre équation
possède au point d'abcisse 2 une tangente parallèle à la droite d'équation y=3x+2: une troisième équation
Deux problèmes indépendants donc:
1) Trouver les trois équations
2) Résoudre le système 3x3 en (a,b,c)
Il ne faut pas oublier que la définition de la dérivée en un point, c'est le coefficient directeur de la tangente en ce point. (c'est très utile ici)
Luc
PS: J'aime bien ta citation!
dérivés
Oui , j'ai trouvé une première équatioon , si Cf passe par A(3;2) alors 2=a*3+b+c/(3-1)
D'ou 3a+b+c/2=2 et 6a+2b+c=4
J'ai aussi trouvé pour les deux autres équations
f'(3)=0 et
f'(2)=3
J'ai essayé d'exprimer f'(3) en sachant que al dérive de f(x)=x est 1 , mais je ne sais pas ce qu'est la dérive de c/(x-1) , et cela donne un calcul trop complique si je passe par f(a+h)-f(a) / h !
N'auriez vous pas une idée?
Ps: merci Luc pour le compliment de citation :)
D'ou 3a+b+c/2=2 et 6a+2b+c=4
J'ai aussi trouvé pour les deux autres équations
f'(3)=0 et
f'(2)=3
J'ai essayé d'exprimer f'(3) en sachant que al dérive de f(x)=x est 1 , mais je ne sais pas ce qu'est la dérive de c/(x-1) , et cela donne un calcul trop complique si je passe par f(a+h)-f(a) / h !
N'auriez vous pas une idée?
Ps: merci Luc pour le compliment de citation :)
Parfait pour les trois équations. Tu as bien compris le lien entre nombre dérivée et coefficient directeur de la tangente.
Maintenant pour pouvoir traduire "f'(3)=0" ou "f'(2)=3"en équation avec a,b,c, le plus simple est de calculer f'(x) pour tout x, avec des formules du cours, sans passer par la limite du taux d'accroissement.
Une fois que tu as calculé f'(x), il suffit de l'évaluer en 2 et 3, et tu as tes trois équations!
PS: La dérivée de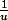 est
est 
Luc
Maintenant pour pouvoir traduire "f'(3)=0" ou "f'(2)=3"en équation avec a,b,c, le plus simple est de calculer f'(x) pour tout x, avec des formules du cours, sans passer par la limite du taux d'accroissement.
Une fois que tu as calculé f'(x), il suffit de l'évaluer en 2 et 3, et tu as tes trois équations!
PS: La dérivée de
Luc
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 96 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
