Détermination d'un ensemble
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 15 Nov 2008, 13:55
par Dimitri22 » 15 Nov 2008, 13:55
Bonjour,
j'ai un petit problèmes à la fin d'un exo.
On a A, B, C et D quatre points non coplanaires. I milieu de [AB], J milieu de [CD] et K milieu de [IJ].
J'ai déjà montrer:
Qu'on ne pouvait pas avoir I=J
Que l'ensemble (1) = {M tq MA+MB=MC+MD} n'a pas de solution (où MA, MB, MC et MD sont des vecteurs)
Que l'ensemble (2)= {M tq ||MA+MB||=||MC+MD||} = plan médiateur de [IJ] (où MA, MB, MC et MD sont des vecteurs)
et je dois trouver l'ensemble (3) = {M tq MA²+MB²=MC²+MD²}
quelqu'un aurait-il une idée?
En sachant que la dernière question est " Peut-on avoir l'ensemble (2) = l'ensemble (3)? " donc il doit y avoir un lien
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 15 Nov 2008, 14:57
par yos » 15 Nov 2008, 14:57
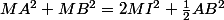
(th. de la médiane, facile à redémontrer avec les propriétés de base du produit scalaire).
Ta condition va devenir
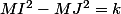
ou encore
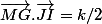
, G étant le milieu de [IJ].
Autre façon : avec un repère.
-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 15 Nov 2008, 21:16
par Dimitri22 » 15 Nov 2008, 21:16
Mais dans ce cas quel est l'ensemble? on ne peut pas le déterminer sans une valeur de k
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 15 Nov 2008, 21:34
par yos » 15 Nov 2008, 21:34
Note H le projeté orthogonal de M sur (IJ). La condition devient
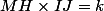
ou
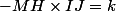
selon le signe de k.
Cette condition détermine le point H. Ainsi les points M solution sont ceux du plan perpendiculaire à (IJ) passant par ce point H.
-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 15 Nov 2008, 21:49
par Dimitri22 » 15 Nov 2008, 21:49
Je ne comprend pas cette étape:
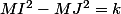
ou encore
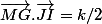
Quand on arrive à
2MI²+(1/2)AB² = 2MJ²+(1/2)CD²
(MI²-MJ²)= (1/4)(CD²-AB²)
je ne vois pas comment passer à MI²-MJ²=k
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 15 Nov 2008, 23:36
par yos » 15 Nov 2008, 23:36
Dimitri22 a écrit: (1/4)(CD²-AB²)
C'est ce que j'ai nommé k : ça ne dépend que de trucs connus. c'est une constante si tu veux.
Ensuite il faut remplacer les carrés des longueurs
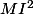
et
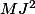
par les carrés des vecteurs

et

puis factoriser la différence des carrés.
-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 15 Nov 2008, 23:58
par Dimitri22 » 15 Nov 2008, 23:58
(\vec{MI}-\vec{MJ})=k)
K milieu de [IJ] donc

Mais je ne vois vraiment pas comment arriver à 2

-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 16 Nov 2008, 00:11
par Dimitri22 » 16 Nov 2008, 00:11
Je viens de trouver. merci

donc au final on a
(CD^2-AB^2))
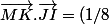(CD^2-AB^2))
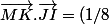(\vec{CD}^2-\vec{AB}^2))
Mais que représente l'ensemble?
-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 16 Nov 2008, 00:32
par Dimitri22 » 16 Nov 2008, 00:32
Dans tous les cas si on a AB=CD dans ce cas l'ensemble (2) = l'ensemble (3)
Mais bon je ne vois pas comment expliquer l'ensemble (3) avec ceci
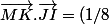(\vec{CD}^2-\vec{AB}^2))
Je pense que l'ensemble serait un point qui dépendrait des coordonnées des point A, B, C et D et donc également des coordonnées de I et J. Est-ce bon?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Nov 2008, 09:20
par yos » 16 Nov 2008, 09:20
J'avais répondu dans le message 4. Ca donne toujours un plan perpendiculaire à (IJ). Comme tu l'as dit, ce plan est le plan médiateur de [IJ] lorsque AB=CD.
-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 16 Nov 2008, 12:27
par Dimitri22 » 16 Nov 2008, 12:27
Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
