Bonjour,
Je commence avec la recurrence et j'ai quelque difficulté (même après avoir regardé bon nombre de messages sur le forum).
Alors, je dois montrer que n^5 - n est divisible par 5
J'ai prouvé que si n = 1 alors 1^5 -1 = 0 donc 0/5 marche
Maintenant on doit le prouver avec n + 1 donc ca nous donne
(n+1) ^5 - (n+1) est divisible par 5
Rendu ici je bloque
Je sais que plus tard je vais devoir dire (n+1) ^5 - (n+1) = 5c et que le triangle de pascal nous aide à calculer le (n + 1) ^5
Mais bon, j'aimerais bien que quelqu'un puisse expliquer la démarche au long
Car la où j'ai de la difficulté est de savoir à quoi arrivé comme réponse à la fin
Merci
Récurrence et divisibilité
10 messages
- Page 1 sur 1
Je commence par te dire que pour une récurrence il faut dire avant la démonstration du rang n+1 qu'on suppose la propriété vrai au rang n
une maniere simple est de développer la formule pour retrouver la propriété au rang n
Allez c'est parti
^{5})
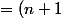^{2}(n+1)^{2}(n+1))
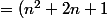(n^{2}+2n+1)(n+1))
apres devellopement et simplification (ou en utilisant dirrectement le triangle de pascal)

et la magie opère
)
le reste tu es capable de le trouver tout seul
une maniere simple est de développer la formule pour retrouver la propriété au rang n
Allez c'est parti
apres devellopement et simplification (ou en utilisant dirrectement le triangle de pascal)
et la magie opère
le reste tu es capable de le trouver tout seul
Merci de la réponse
J'en profite pour en poser un autre toute bête qui me tracasse
Sur se site il y a une démonstration de divisibilité
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divisi5.htm#div5
J'arrive pas à comprendre pourquoi l'auteur, lorsqu'il est à son étape de
calculer la différence, il fait f(n+1) - 2*f(n)
Pourquoi ce n'est pas moins f(n) ?
Merci
J'en profite pour en poser un autre toute bête qui me tracasse
Sur se site il y a une démonstration de divisibilité
http://villemin.gerard.free.fr/Wwwgvmm/Decompos/Divisi5.htm#div5
J'arrive pas à comprendre pourquoi l'auteur, lorsqu'il est à son étape de
calculer la différence, il fait f(n+1) - 2*f(n)
Pourquoi ce n'est pas moins f(n) ?
Merci
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

