Résolution équation avec arrangements
14 messages
- Page 1 sur 1
Résolution équation avec arrangements
Bonjour (je réédite mon message car j'ai bloqué par inadvertance ma dernière discussion).
C'est une équation avec des arrangements que j'écris A(n;p)
Il faut résoudre l'équation suivante en déterminant n :
A(2n;2)-14=A(n;2)
merci beaucoup.
C'est une équation avec des arrangements que j'écris A(n;p)
Il faut résoudre l'équation suivante en déterminant n :
A(2n;2)-14=A(n;2)
merci beaucoup.
réponse
et bien moi aussi g bloque c pourquoi g demande : g essayer de transformer en une équation du second degré mais delta est négatif???
réponse à flight
Oui c'est une bonne piste et l'avantage est que ton delta est positif.
Soit à résoudre
à résoudre
on trouve delta =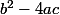
Soit delta =) = 169
= 169
Comme on travaille sur des arrangements, on ne peut prendre que la racine positive soit :
n =/6) =
= 
Mais la solution est décimale et n ne peut appartenir qu'à N*. Donc ce n'est pas ca non plus.
Des idées................?! :marteau:
Soit
on trouve delta =
Soit delta =
Comme on travaille sur des arrangements, on ne peut prendre que la racine positive soit :
n =
Mais la solution est décimale et n ne peut appartenir qu'à N*. Donc ce n'est pas ca non plus.
Des idées................?! :marteau:
Réponse
Monsieur le modérateur, il faut peut être pas pousser non plus, je vais pas écrire toutes mes équations en TEX, c'est déjà dur de comprendre les mathématiques, alors apprendre la programmation informatique, il ne faut pas pousser. Depuis, 3 jours que je suis sur ce site, tout le monde écrit comme moi.
Sinon, pour les autres, n doit forcément être un entier naturel, donc nous avons du partir sur une mauvaise piste. C'est un sujet d'examen, il y a forcément une solution de n en entier naturel et j'ai l'original de l'énoncé. Mais il est vrai que c'est dur! J'ai encore fait d'autres essais, mais je ne trouve pas.
Sinon, pour les autres, n doit forcément être un entier naturel, donc nous avons du partir sur une mauvaise piste. C'est un sujet d'examen, il y a forcément une solution de n en entier naturel et j'ai l'original de l'énoncé. Mais il est vrai que c'est dur! J'ai encore fait d'autres essais, mais je ne trouve pas.
pierre71 a écrit:Monsieur le modérateur, il faut peut être pas pousser non plus, je vais pas écrire toutes mes équations en TEX, c'est déjà dur de comprendre les mathématiques, alors apprendre la programmation informatique, il ne faut pas pousser.
Il y'a une différence entre écrire en tex et écrire en sms.
Ici on est pas sur un portable, mais sur un forum de discussion, un minimum de courtoisie s'impose.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
