Polynome
14 messages
- Page 1 sur 1
Polynome
Bonjour, j'ai un dm de maths a faire, et je bloque sur certaine questions...
Merci d'avance pour votre aide.
Déterminé tous les polynomes de degré 2 ayant pour racines -5 et 2 et dont l'image de zéro est 1
VRAI- FAUX justifier:
L'équation (x² -4x +3)/(x-1)= 0 a pour ensemble de solution S= {1;3}
Merci d'avance pour votre aide.
Déterminé tous les polynomes de degré 2 ayant pour racines -5 et 2 et dont l'image de zéro est 1
VRAI- FAUX justifier:
L'équation (x² -4x +3)/(x-1)= 0 a pour ensemble de solution S= {1;3}
Bonjour, c'est parti pour l'aide, tu dois utiliser les différentes information qui te sont données
Tout d'abord qu'est ce qu'un ploynome de seconde degré?
c'est un polynome qui s'écrit sous la forme:

avec a,b,c des nombres réels, a étant non nul
Ensuite qu'est ce que veut dire que l'image de zéro est 1?
cela veut dire qu'en remplaçant X par 0 dans l'équation donnée, tu obtiens 1
ainsi on a

donc
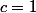
ensuite tu sais que -5 et 2 sont les racines de ce polynome
ainsi en utilisant les données déja exploitées
et en traduisant la définition des racines numériquement
^{2}a + -5b + 1 = 0)

il suffit donc de résoudre ce petit système de deux équation et de voir si il y a plusieurs résultats
Tout d'abord qu'est ce qu'un ploynome de seconde degré?
c'est un polynome qui s'écrit sous la forme:
avec a,b,c des nombres réels, a étant non nul
Ensuite qu'est ce que veut dire que l'image de zéro est 1?
cela veut dire qu'en remplaçant X par 0 dans l'équation donnée, tu obtiens 1
ainsi on a
donc
ensuite tu sais que -5 et 2 sont les racines de ce polynome
ainsi en utilisant les données déja exploitées
et en traduisant la définition des racines numériquement
il suffit donc de résoudre ce petit système de deux équation et de voir si il y a plusieurs résultats
Pour la deuxième question c'est une question de bon sens,
Sachant qu'il y a pour un polynome de seconde degré, dans R, au maximum deux racines différentes
Il suffit de remplacer dans le polynme x par les valeurs des racines pour vérifier si ce polynome possède comme racine ces deux nombre.
Attention: il faut vérifier si en remplaçant par ces nombres l'opération que tu vas effectuée est possible ou pas aussi, un polynome de second degrès peut avoir une seule racine ou aucune dans R
Sachant qu'il y a pour un polynome de seconde degré, dans R, au maximum deux racines différentes
Il suffit de remplacer dans le polynme x par les valeurs des racines pour vérifier si ce polynome possède comme racine ces deux nombre.
Attention: il faut vérifier si en remplaçant par ces nombres l'opération que tu vas effectuée est possible ou pas aussi, un polynome de second degrès peut avoir une seule racine ou aucune dans R
Rebonjour,
Déterminer tous les polynômes de degré 2 ayant pour racines -5 et 2 et dont l'image de zéro est 1
Un polynôme qui a pour racine -5 et 2 peut se factoriser sous la forme(x+5)(x-2)Q(x)
comme le degré de (x+5)(x-2) est 2 le degré de Q est 0
donc Q est un nombre réel non nul
maintenant P(0) = 1
donc (5)(-2)Q = 1 ou -10Q = 1 Q = -1/10
Le seul polynôme qui réponde à ces trois conditions est
P(x) = -1/10 (x+5)(x-2)
Réfléchir fait gagner du temps ! Avant de se lancer dans des calculs, commencer par raisonner et voir si la réponse n'est pas évidente...
Bonne soirée
Déterminer tous les polynômes de degré 2 ayant pour racines -5 et 2 et dont l'image de zéro est 1
Un polynôme qui a pour racine -5 et 2 peut se factoriser sous la forme(x+5)(x-2)Q(x)
comme le degré de (x+5)(x-2) est 2 le degré de Q est 0
donc Q est un nombre réel non nul
maintenant P(0) = 1
donc (5)(-2)Q = 1 ou -10Q = 1 Q = -1/10
Le seul polynôme qui réponde à ces trois conditions est
P(x) = -1/10 (x+5)(x-2)
Réfléchir fait gagner du temps ! Avant de se lancer dans des calculs, commencer par raisonner et voir si la réponse n'est pas évidente...
Bonne soirée
Merci beaucoup pour votre aide! C'est beaucoup plus simple de cette maniere la en effet...
Maintenant j'ai:
Soit le polynome: P(x) = 2 x^3 +15 x²- 2673
1- Quel est le degré de P(x)? Quel sont ces coefficients?
> Le degré de P(x) est 3
> Coefficients, non resolu
2- Démontrer que 9 est une racince de P(x)
>P(9) = 2*9^3 +15*9²-2673
= 1458 + 1215-2673
= 0
Conclusion: 9 est bien racine de P(x)
3-Factoriser au maximum P(x)
>non résolu
4- Déduire les solutions de l'equations P(x)=0
> non résolu
Pouvez vous m'aider svp?
Maintenant j'ai:
Soit le polynome: P(x) = 2 x^3 +15 x²- 2673
1- Quel est le degré de P(x)? Quel sont ces coefficients?
> Le degré de P(x) est 3
> Coefficients, non resolu
2- Démontrer que 9 est une racince de P(x)
>P(9) = 2*9^3 +15*9²-2673
= 1458 + 1215-2673
= 0
Conclusion: 9 est bien racine de P(x)
3-Factoriser au maximum P(x)
>non résolu
4- Déduire les solutions de l'equations P(x)=0
> non résolu
Pouvez vous m'aider svp?
Tu peux aussi te dire que:
a=2, seule possibilité pour avoir 2x^3, car 2x^2(x-9)=2x^3-18x^2
Apres, tu veux 15 x^2, mais tu as déjà (-18 x^2). Il faut donc que b=33 pour avoir 15 x^2 car (2x^2+33x)(x-9)=2x^3+15x^2-297x
Apres, tu n'as aucun terme de rang 1.
c=297, pour contrebalancer les -297x "crées" par le b=33
et la, Ô miracle, tout tombe juste.
a=2, seule possibilité pour avoir 2x^3, car 2x^2(x-9)=2x^3-18x^2
Apres, tu veux 15 x^2, mais tu as déjà (-18 x^2). Il faut donc que b=33 pour avoir 15 x^2 car (2x^2+33x)(x-9)=2x^3+15x^2-297x
Apres, tu n'as aucun terme de rang 1.
c=297, pour contrebalancer les -297x "crées" par le b=33
et la, Ô miracle, tout tombe juste.
mathilde36 a écrit:Merci beaucoup pour votre aide! C'est beaucoup plus simple de cette maniere la en effet...
Maintenant j'ai:
Soit le polynome: P(x) = 2 x^3 +15 x²- 2673
1- Quel est le degré de P(x)? Quel sont ces coefficients?
> Le degré de P(x) est 3
> Coefficients, non resolu
2- Démontrer que 9 est une racince de P(x)
>P(9) = 2*9^3 +15*9²-2673
= 1458 + 1215-2673
= 0
Conclusion: 9 est bien racine de P(x)
3-Factoriser au maximum P(x)
>non résolu
4- Déduire les solutions de l'equations P(x)=0
> non résolu
Pouvez vous m'aider svp?
Ton polynome de degres trois est
2 x^3 +15 x²- 2673
A comparer avec un polynome de degre 3 general
a x^3 + b x^2 + c x + d Ou a, b, c, et d sont les coefficients de ton polynome.
Factoriser au maximum 1) Divison Euclidienne ou 2) Avoir le nez.
Tu sais que si 9 est une racine, tu peux ecrire que
(x-9)(ax^2+bx+c) = 2x^3 + 15x^2 - 2673
C'est juste la traduction de : Si 9 est une racine, je peux sortir un facteur (x-9) de mon expression.
Mais, je ne sais pas a quoi ressemble mon expression avec un facteur (x-9) sorti, si ce n'est que je sais que le reste doit etre de degre 2.
Il te reste a determiner les coefficients a, b, et c de ton polynome.
Pour cela, un peu de bon sens.
(x-9)(ax^2+bx+c) = 2x^3 + 15x^2 - 2673
Tu sais que la seule combinaison qui va te donner une puissance ^3 est la combinaison x*ax^2 e.g le premier terme de la distribution.
Par consequent, tu deduis que a = 2
Tu sais que la seule combinaison qui donne le dernier facteur est la combinaison -9 * c e.g le dernier terme de la distribution
Donc c = 297
Tu as donc
(x-9)(2x^2 + bx + 297) = 2x^3 - 15x^2 - 2763
=
2x^3 + bx^2 + 297x - 18x^2 - 9bx - 2763
Tu sais que tu ne veux pas de termes en x, car il n'y en a pas dans ton polynome
Donc -297x = -9bx
b = 33
Si tu as fait ton raisonnement juste, tu peux aussi verifier que
bx^2 - 18x^2 = 15x^2
Donc que b = 33 ici aussi
Si ca te plait pas, passe par la divison Euclidienne si t'as le droit
Tu as donc (x-9)(2x^2+33x+297) = 2x^3 + 15x - 2673
Tu veux encore factoriser plus
Utilise le determinant pour factoriser 2x^2 + 33x + 297
Bizarre... C'est pas possible de le factoriser...
Ca veut dire quoi pour ses racines?
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
