équation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
dodie181
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Jan 2008, 20:26
-
 par dodie181 » 12 Nov 2008, 14:52
par dodie181 » 12 Nov 2008, 14:52
Bonjour,
j'aimerai savoir si ce que j'ai commencé est bon ?
mon équation est sqrt{x^2-x-6} = sqrt{x-1}
sqrt{x^2-x-6} = sqrt{x-1}
sqrt{x^2-x-6}^2 = sqrt{x-1}^2
x^2-x-6= x-1
x^2-x-6-x+1=0
x^2-2x-5=0
ensuite je calcule le discriminant
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 12 Nov 2008, 14:54
par Timothé Lefebvre » 12 Nov 2008, 14:54
Salut, d'accord et tu trouves quoi comme discriminant ?
-
dodie181
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Jan 2008, 20:26
-
 par dodie181 » 12 Nov 2008, 14:56
par dodie181 » 12 Nov 2008, 14:56
je trouve 24 pour le discriminant et j ai donc 2 solutions
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 12 Nov 2008, 15:04
par Timothé Lefebvre » 12 Nov 2008, 15:04
Tout à fait.
Quelles sont les solutions ?
D'abord sous forme littérale puis ensuite avec les valeurs du problème.
-
j_e
- Membre Naturel
- Messages: 70
- Enregistré le: 02 Nov 2008, 11:08
-
 par j_e » 12 Nov 2008, 15:07
par j_e » 12 Nov 2008, 15:07
Mmmhhh ... Un petite remarque en passant ... Un bon réflexe à avoir lorsqu'on rencontre des racines est de déterminer les conditions d'existence de l'équation.
(pour rappel, une expression soumise à une racine d'indice pair doit être positive!)
Bon travail !
-
dodie181
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Jan 2008, 20:26
-
 par dodie181 » 12 Nov 2008, 15:09
par dodie181 » 12 Nov 2008, 15:09
(-b-racine de delta)/2a et (-b+racine de delta)/2a
(2-racine 24)/2 (2+racine 24)/2
désolé s'est écrit en lettre mais je n'arrive pas utilisé les balises
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 12 Nov 2008, 15:13
par Timothé Lefebvre » 12 Nov 2008, 15:13
Soit

le discriminant tel qu'ici

> 0
Que sont les deux racines réelles de ce polynôme ?
-
dodie181
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Jan 2008, 20:26
-
 par dodie181 » 12 Nov 2008, 15:15
par dodie181 » 12 Nov 2008, 15:15
les deux racines réelle sont (2-racine 24)/2 et (2+racine 24)/2 ?
-
dodie181
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Jan 2008, 20:26
-
 par dodie181 » 12 Nov 2008, 15:21
par dodie181 » 12 Nov 2008, 15:21
1-2racine6 et 1+2racine6
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 12 Nov 2008, 15:24
par Timothé Lefebvre » 12 Nov 2008, 15:24
Hum ...
Moi j'ai trouvé

et

, tu t'es trompée dans ta simplification.
-
dodie181
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Jan 2008, 20:26
-
 par dodie181 » 12 Nov 2008, 15:31
par dodie181 » 12 Nov 2008, 15:31
a oui j ai trouver mon erreur ! et est ce que l ensemble de définition de mon équation est bien Df= R+/1
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 12 Nov 2008, 15:33
par Timothé Lefebvre » 12 Nov 2008, 15:33
Hum ... Réfléchis et regarde bien les deux racines.
-
dodie181
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Jan 2008, 20:26
-
 par dodie181 » 12 Nov 2008, 15:40
par dodie181 » 12 Nov 2008, 15:40
x²-x-6>0 x-1>0
x²-x>6 x>1
x>-6
est ce correcte pour x²-x-6 ?
-
j_e
- Membre Naturel
- Messages: 70
- Enregistré le: 02 Nov 2008, 11:08
-
 par j_e » 12 Nov 2008, 16:42
par j_e » 12 Nov 2008, 16:42
Non ... En fait, tu as

Ce qui est une
condition sur le signe d'une expression. Pour déterminer quand cette condition est vraie (ce qui nous intéresse), il suffit d'établir le tableau de signe de l'expression, ici
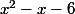
. Il suffit enfin de voir pour quelles valeurs de x l'expression
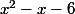
est positive.
Bon courage !
(par contre,

est bien juste

)
-
dodie181
- Membre Naturel
- Messages: 11
- Enregistré le: 27 Jan 2008, 20:26
-
 par dodie181 » 12 Nov 2008, 16:51
par dodie181 » 12 Nov 2008, 16:51
d 'accord merci beaucoup de vos aides
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités

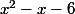 . Il suffit enfin de voir pour quelles valeurs de x l'expression
. Il suffit enfin de voir pour quelles valeurs de x l'expression 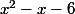 est positive.
est positive. est bien juste
est bien juste  )
)