Question sur dérivée

[idrys]

Bonjour , j'ai un petit problème sur une dérivée si quelqu'un pouvait m'aider sa serai gentil :)

F(t) = 8.25te^-t ( e^-t veut dire exp(-t) )

Voila donc j'ai la formule (uv) ' = u'v+v'u

Ece que je peux prendre u= 8.25t et v= exp(-t) ?

[Kah]

Oui, tu peux! Enfin, tu dois!

[j_e]

Oui, bien sur !

[idrys]

Ok merci .

Parce que j'hésitais entre u= 8.25t , v = exp(-t) et u=8.25 , v = te^-t

[j_e]

En fait, ce que tu peux aussi faire, c'est ceci :

( : on peut "sortir d'une dérivée" une constante multiplicative)

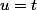
Il te reste alors à dériver , et là, tu appliques la formule du produit en prenant et

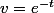
Ok ?

Bon travail !

[Kah]

Heu choisir u(x)= 8.25, il y a plus astucieux :ptdr:
Au pire, tu poses F(t)=8,25(uv)
Avec u(t)=t
et v(t)=e^(-t)
donc F'(t)=8,25(u'v+uv')

[idrys]

J'y suis arrivai en prenant

u= 8.25t v= exp(-t)

Formule (uv)'= u'v + v'u

u'= 1 et v' = -exp(-t)

Donc : f'(t) = 1 * exp(-t) + (-exp(-t) * 8.25t )
= exp(-t) + (-8.25texp(-t))
= exp (- t) * ( 1 - 8.25 t)

Voila pour ma dérivée

[idrys]

c'est juste ?

[j_e]

Non ! Attention !



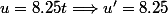
Formule :
Si k : constante réelle et f : fonction :

[idrys]

A ok merci du renseignement , sa je l'ignorai

Donc alors sa donne

u= 8.25t u'=8.25
v=exp(-t) v'=-exp(-t)

f'(t)= 8.25 * exp(-t) + (-exp(-t)) * 8.25t
= 8.25e^-t - 8.25te^-t
= 8.25 * ( e^(-t) - te^(-t) )

C'est juste ?

[j_e]

Ouaip ! Impek ;-)

[idrys]

Merci pour l'aide :)