Integration de sinx/x
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
bibup
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2006, 09:49
-
 par bibup » 11 Nov 2008, 22:37
par bibup » 11 Nov 2008, 22:37
bonjour a tous,
je dois calculer
}{x}dx)
mais l'enoncé me guide.
1)
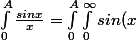 exp(-xt) dxdt)
2) Calculer
=\int_0^Asin(x) exp(-xt) dx)
3) En déduire que
}{x}dx=\pi/2)
Je suis arrivée a faire la question 1, j'ai trouvé pour la question 2 que I
=\frac{1}{1+t^2} - \frac{(cos(A)+tsin(A))exp(-At)}{t^2+1})
et voila ce que je trouve pour la question 3 :
}{x}dx=[arctan]-\int_0^\infty \lim\limits_{A \rightarrow \infty} \frac{(cos(A)+tsin(A))exp(-At)}{t^2+1}dt)
et arcten entre 0 et l'infini vaut
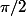
mais pourquoi l'autre partie de l'integrale vaut 0?
Merci pour votre aide

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 11 Nov 2008, 22:52
par Sa Majesté » 11 Nov 2008, 22:52
Bonjour,
Tu peux majorer la valeur absolue de l'intégrale par l'intégrale de la valeur absolue
Puis la valeur absolue de cos par 1, idem pour sin
Tu finis par majorer la valeur absolue de l'intégrale par qqch qui converge vers 0 qd A tend vers +oo
... si je ne me suis pas trompé !
-
bibup
- Membre Naturel
- Messages: 27
- Enregistré le: 29 Oct 2006, 09:49
-
 par bibup » 11 Nov 2008, 23:22
par bibup » 11 Nov 2008, 23:22
+tsin(A))exp(-At)}{t^2+1}dt| \leq \int_0^\infty \lim\limits_{A \rightarrow \infty} |\frac{(cos(A)+tsin(A))exp(-At)}{t^2+1}|dt)
+tsin(A)|exp(-At)}{t^2+1}dt)
exp(-At)}{t^2+1}dt)
car cos<1 et sin<1
mais la voila je ne sais plus
Merci d'avance pour votre aide
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 11 Nov 2008, 23:28
par Luc » 11 Nov 2008, 23:28
Bonsoir,
je suis peut-être hors-sujet mais il me semble que c'est plus la limite de l'intégrale que l'intégrale de la limite. Il faut peut-être appliquer Fubini avant de passer à la limite. En effet,
+tsin(A))exp(-At)}{t^2+1}dt)
ne me paraît pas avoir grand sens (j'espère me tromper). Quel est le sens à donner à cette limite? Convergence simple? Uniforme en t ?
Ceci dit la majoration marche de la même façon
Cordialement,
Luc

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 12 Nov 2008, 20:19
par Sa Majesté » 12 Nov 2008, 20:19
[quote="bibup"]
+tsin(A))exp(-At)}{t^2+1}dt| \leq \int_0^\infty \lim\limits_{A \rightarrow \infty} |\frac{(cos(A)+tsin(A))exp(-At)}{t^2+1}|dt)
+tsin(A)|exp(-At)}{t^2+1}dt)
exp(-At)}{t^2+1}dt)
car cos[/U] 0

par exemple :id:
PS : je suis d'accord avec Luc : majorer l'intégrale puis prendre la limite
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités