Probabilité : montrer que f borelienne

[jeremy58]

Bonjour,
je suis en train de réviser pour mon partiel, et j'ai un exo de mon TD que je ne comprends pas.
Voila l'énoncé :

Soit f:R²->R,
on suppose que
pour x R fixé, y->f(x,y) borélienne
pour y x-> f(x,y) continue.
Montrer que (x,y)->f(x,y) est borélienne

Voila ce que le prof a donné comme correction :
On a

et

Voila je comprends pas pourquoi on prend un sous cette forme et en quoi cela répond a la question.
Merci d'avance pour votre aide

[Maxmau]

Bj
Soit ;) une constante
La fonction (x,y) ----- > f( ;),y) est borélienne
;)n est construite avec des fonctions de ce type de sorte qu’elle est borélienne
La fonction (x,y) ---- > f(x,y) est alors borélienne comme limite de fonctions boréliennes

[ffpower]

et le passage a la limite utilise la continuité..
Cela dit ca semble un peu barbare ecrit comme ca,doit y avoir un moyen de refaire ca plu proprement

[jeremy58]

Merci pour vos reponses, je comprends un petit peu mieu meme s'il reste plusieurs endroit encore un peu flou.
Premierement, pourquoi ce il fallait prevoir a l'avance que allait tendre vers f(x,y)?
Ensuite, pourquoi cette limite vaut f(x,y)? Est-ce que c'est a ce moment qu'on doit utiliser que la limite du tend vers 0?
Merci d'avance pour vos reponses

[Maxmau]

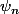
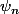
Premierement, pourquoi ce il fallait prevoir a l'avance que allait tendre vers f(x,y)?
Merci d'avance pour vos reponses

Elle est construite pour ça

Ensuite, pourquoi cette limite vaut f(x,y)? Est-ce que c'est a ce moment qu'on doit utiliser que la limite du tend vers 0?
Merci d'avance pour vos reponses

Oui
voir indic ci-après


Je note a(k,n) et J(k,n) = [a(k,n) , a(k+1,n) [
Remarque qu’on peut prendre par exemple : a(k,n) = k/n

Je pose A(k,n,x) = (a(k+1,n) – x )/( a(k+1,n) - a(k,n))
Alors :
n(x,y) = [A(k,n,x) f(a(k,n),y) + (1- A(k,n,x) f(a(k+1,n),y)] 1J(k,n)(x)
Remarque que x,y,n étant donnés, il existe un unique k’ tel que
x soit dans J(k’,n) d’où :
n(x,y) = A(k’,n,x) f(a(k’,n),y) + (1- A(k’,n,x) f(a(k’+1,n),y)

Il est intéressant aussi de remarquer alors que :
f(x,y) = [A(k,n,x) f(x,y) + (1- A(k,n,x) f(x,y)] 1J(k,n)(x)
= A(k’,n,x) f(x,y) + (1- A(k’,n,x) f(x,y)

Soit (x,y) et soit > 0
La continuité de f /x et les propriétés des a(k,n) permettent de montrer que pour n assez grand | n(x,y) – f(x,y)| <