leon1789 a écrit:héé l'eau !
la difficulté n'est pas de dire ce que vaut
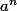
avdc
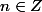
, voire
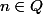
, mais de justifier des propriétés avec des exposants
réels, non ?
C est d ailleurs un autre moyen de finir l exponentielle,plus intuitif(pas forcément plus pratique):
Si a>0, on sait définir
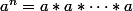
pour n dans N*.Ca vérifie la propriété fondamentale (P):
^n)
.
On peut définir ensuite
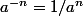
ce qui permet de définir
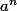
pour n dans Z de facon a ce que (P) soit respectée.
D autre part,on prouve que si n est dans N*,l application
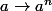
est une bijection continue strictement croissante de R dans R,ce qui permet de définir la racine n-ieme.
On pose alors
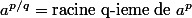
.On vérifie
que
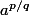
ne dépend de p et q que par p/q puis que (P) est encore vérifiée sur les rationnels.Pour a>0,on a donc défini
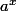
sur tous les rationnels.
Finalement,si x est réel,on vérifie que si
)
est une suite de rationnels qui tend vers x,alors
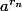
converge vers une limite qui ne dépend pas de
)
,ce qui permet de définir
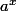
pour tout réel x,et (P) est encore vérifiée sur les réels.
Pour finir,on vérifie que la fonction
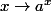
est dérivable sur R(ca,ca n est a priori pas tres facile.J ai une méthode facile en intégrant la relation
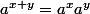
par rapport a y sur un intervalle,mais je sais pas si ya une méthode élémentaire(probablement))
On montre que la dérivée de cette fonction est proportionnelle à la fonction elle meme,on note ln(a) cette proportion.
Une étude rapide de ln montre qu il existe un unique a tel que ln(a)=1,autrement dit il n y a qu une seule valeur de a telle que
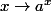
soit sa propre dérivée.Ce qui permet de définir e et de récupérer toutes les propriétés que l on connait
