Résoudre 2 équations (trouver x )

[polin]

Bonjour,
j'ai deux équations qui me posent problème, il faut trouver x dans les deux cas :

a) 2(3x - 1)(x - 8)+(5x - 2)(-3x + 1) - (3x - 1) = (12x - 4)²


.....5x - 2.....4x - 7......4x + 1
b) ______ - ______ = ______- x
........3...........6............2


*j'ai écrit les fractions comme j'ai pu*

Merci d'avance de votre aide
(les deux équations sont distinctes, je précise).

[Sve@r]

Bonjour,
j'ai deux équations qui me posent problème, il faut trouver x dans les deux cas :

a) 2(3x - 1)(x - 8)+(5x - 2)(-3x + 1) - (3x - 1) = (12x - 4)²


.....5x - 2.....4x - 7......4x + 1
b) ______ - ______ = ______- x
........3...........6............2

a) tu développes, tu réduis, tu obtiens une équation du 2° degré à une inconnue

b) tu mets toutes les fractions au même dénominateur => plus de fraction

*j'ai écrit les fractions comme j'ai pue*

"pu" du verbe pouvoir et non "pue" du verbe puer => http://maths-forum.com/showthread.php?t=70548

[polin]

J'ai essayé de toutes les manières possible de développer ou de factorisé la a), mais je n'y arrive pas, c'est bien pour cette raison que je demande de l'aide. La théorie je connais, mais la pratique me pose problème sur ce calcul.
Pour la b), je ne vois pas du tout comment les fractions peuvent disparaitre si je les mets sur le même dénominateur. Lorsque je fais le calcul en mettant tout au même dénominateur, je me retrouve avec comme réponse 0 = 16/6, ce qui est impossible.

Merci de me donner de plus amples explications.

[fibonacci]

Bonjour;

[fibonacci]

soit



le dénominateur commun est 6

en réduisant au même dénominateur on a




je n'ai rien changé, l'égalité est respectée et si je simplifie terme à terme on retombe bien sur l'expression de départ.

maintenant si je multiplie par 6 l'expression à droite et à gauche de la dernière égalité nous avons:



l'égalité est respecté



en définitif on a 2a+3b=6c

ce que je viens de faire on le fait de façon sous entendue .

donc à toi de jouer...après avoir simplifier

on a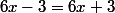

0=6 solution impossible

[Sve@r]

J'ai essayé de toutes les manières possible de développer ou de factorisé la a), mais je n'y arrive pas, c'est bien pour cette raison que je demande de l'aide. La théorie je connais, mais la pratique me pose problème sur ce calcul.
Pour la b), je ne vois pas du tout comment les fractions peuvent disparaitre si je les mets sur le même dénominateur. Lorsque je fais le calcul en mettant tout au même dénominateur, je me retrouve avec comme réponse 0 = 16/6, ce qui est impossible.

Merci de me donner de plus amples explications.

Bon, contrairement aux règles, fibonacci t'a solutionné complètement l'exercice donc je ne peux plus rien dire. Mais contrairement à ta fausse idée, il arrive qu'un système d'équations n'ait aucune solution.
Exemple
x+y=5
2x+2y=10

x+y=5
2x+2y=12

Dans les deux cas, on ne trouve rien de concret. Le premier parce que les équations sont identiques, le second parce qu'elles ont les mêmes facteurs mais une égalité différente.

Si on représentait ces équations graphiquement, dans le second cas on aurait deux droites parallèles et dans le premier, deux droites confondues. Mais dans les deux cas on ne peut pas trouver un unique point commun aux deux. Dans le premier il y en a une infinité et dans le second aucun.

Pour savoir si un système admet une solution unique, il faut multiplier les facteurs en croix. Si le résultat est égal, alors il n'a pas de solution.
Dans mes exemples, 2 * 1 = 4 et 1 * 2 = 4 donc pas de solution.

Mais si j'avais eu
x+2y=5
2x+y=10
Alors 2 * 2 = 4 et 1 * 1 = 1 => résultats différents => le système a une solution qui peut être trouvée

[fibonacci]

Bonjour;

Je sais, mais cela doit permettre de suivre le cheminement et par là, à lever le doute sur la façon d’aborder se type d’équation.
C’est vrai aussi que s’il se contente d’une simple recopie alors, c’est peine perdue.