Limites de suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
david-james
- Membre Naturel
- Messages: 11
- Enregistré le: 21 Mai 2008, 21:49
-
 par david-james » 05 Nov 2008, 18:23
par david-james » 05 Nov 2008, 18:23
Bonsoir, est-ce que quelqu'un pourrait m'aider, je n'arrive pas à faire une question de cet exercie:
Soit une suite Un définie par U0= 3 et par la relation Un+1=3Un-4 pour n appartenant N
1) Quelle est la limite réelle l éventuelle de cette suite ?
Celle ci je l'ai faite, je trouve l=2
2)On pose alors Vn=Un-l pour tout entier naturel n. Montrer que la suite (Vn) est une suite géométrique dont on donnera la limite. Celle-ci je n'y arrive pas. Quand j'exprime Vn+1 en fonction de Vn, je trouve Vn+1= Un+1-l= 3Un-4-l
Je ne vois pas comment ensuite arriver à exprimer Vn+1 en fonction de Vn avec ceci.
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 05 Nov 2008, 18:35
par L.A. » 05 Nov 2008, 18:35
Bonjour.
dans la deuxième question on sait que l=2
et ça aide...
-
david-james
- Membre Naturel
- Messages: 11
- Enregistré le: 21 Mai 2008, 21:49
-
 par david-james » 05 Nov 2008, 18:40
par david-james » 05 Nov 2008, 18:40
Ah oui je vois, ça me donne Vn+1 = 3Un-4-2 = 3Un-2, or Vn = Un -2 mais il y a le 3, ce n'est pas 3( Un-2 ) :( Alors comment faire ?
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 05 Nov 2008, 18:41
par L.A. » 05 Nov 2008, 18:41
petite erreur de calcul au grosses conséquences...
-4-2 = -6 et pas -2
(je sais j'ai failli faire la même...)
-
Kah
- Membre Rationnel
- Messages: 540
- Enregistré le: 15 Sep 2008, 19:51
-
 par Kah » 05 Nov 2008, 18:42
par Kah » 05 Nov 2008, 18:42
Attention! -4-2=-6, pas "-2"!!!
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 05 Nov 2008, 18:42
par L.A. » 05 Nov 2008, 18:42
Petite erreur :
-4-2 = -6 et pas -2
(je sais j'ai failli faire la même)
-
david-james
- Membre Naturel
- Messages: 11
- Enregistré le: 21 Mai 2008, 21:49
-
 par david-james » 05 Nov 2008, 18:47
par david-james » 05 Nov 2008, 18:47
Oups, ah oui ça change tout ^^ Merci beaucoup. Mais pour chercher la limite de Vn, est-ce que V0 il faut le chercher ? Ou il ne change rien ? Moi, j'aurais tendance a ne pas le chercher lol enfin je pense qu'il ne change rien c'est par rapport juste à la raison, au 3^n non ??
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 05 Nov 2008, 18:54
par L.A. » 05 Nov 2008, 18:54
Vn est donc une suite géométrique de raison 3
selon la valeur de la raison, il peut se faire qu'on puisse conclure directement à la question de la convergence, sans calcyuler V0. Peut-on ici, et pourquoi ?
-
david-james
- Membre Naturel
- Messages: 11
- Enregistré le: 21 Mai 2008, 21:49
-
 par david-james » 05 Nov 2008, 18:58
par david-james » 05 Nov 2008, 18:58
J'ai écrit que Vn est une suite de raison 3, donc Vn=V0xq^n = V0x3^n.
Or 3 plus grand que 1 donc lim Vn = + l'infini n
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 06 Nov 2008, 11:17
par L.A. » 06 Nov 2008, 11:17
J'ai tendu le piège tout exprès... :zen:
si on a une raison |q|>1, il peut se trouver que la suite Vn = V0 q^n converge (lorsque V0 prend une valeur bien précise ...)
donc la situation n'est pas si simple et il faut bien calculer V0.
-
tigre
- Membre Relatif
- Messages: 176
- Enregistré le: 02 Oct 2008, 18:09
-
 par tigre » 06 Nov 2008, 15:42
par tigre » 06 Nov 2008, 15:42
david-james a écrit:Bonsoir, est-ce que quelqu'un pourrait m'aider, je n'arrive pas à faire une question de cet exercie:
Soit une suite Un définie par U0= 3 et par la relation Un+1=3Un-4 pour n appartenant N
1) Quelle est la limite réelle l éventuelle de cette suite ?
Celle ci je l'ai faite, je trouve l=2
2)On pose alors Vn=Un-l pour tout entier naturel n. Montrer que la suite (Vn) est une suite géométrique dont on donnera la limite. Celle-ci je n'y arrive pas. Quand j'exprime Vn+1 en fonction de Vn, je trouve Vn+1= Un+1-l= 3Un-4-l
Je ne vois pas comment ensuite arriver à exprimer Vn+1 en fonction de Vn avec ceci.
t'es presque
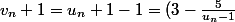(v_n))
-
david-james
- Membre Naturel
- Messages: 11
- Enregistré le: 21 Mai 2008, 21:49
-
 par david-james » 06 Nov 2008, 18:20
par david-james » 06 Nov 2008, 18:20
Ah d'accord. Merci beaucoup pour vos aides :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
