[Terme S]Limite de suite

[hgaet]

Bonjour à tous, je suis bloqué à une fin d'exercice, sur 2 questions.

Enoncé
On définit la suite (un) sur N par (un)=f[n*(pi/2)]
On sait que f(x)=e(-x) cos (4x)

a) Montrer que la suite (un) est une suite géométrique et préciser sa raison.
b) En déduire le sens de variation de la suite (un) et étudier sa convergence.


Pour la b) j'ai étudier la limite de f(x) en + infini, ca fait 0, mais la limite de (n*pi/2) en + infini ça fait + infini. Est-ce que le tout tend vers 0 ?

Merci d'avance pour votre aide

[Monsieur23]

Aloha ;

Oui, c'est bon pour la b).
Il faut tout de même que tu précises que f est continue.

As-tu réussi la a) ?

[hgaet]

Non pas la a)

Mais je suppose que si j'ai la a), j'aurai facilement le sens de variation de (un)

[Monsieur23]

Ok.

Donc pour tout n,

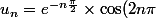A quoi est égal ?

[hgaet]

cos (2n pi) est égale soit à 1 soit à -1

[Monsieur23]

Non, c'est toujours égal à 1 ( regarde bien le cercle trigonométrique : 2npi revient à faire n tours, mais au final on se retrouve toujours au début).

Maintenant, tu dois trouver une forme géométrique, c'est à dire de la forme a^n.
Que vaut a ici ?

[hgaet]

:look: oula ... C'est toujours égale à 1 ça ok.

Mais pour trouver une forme géométrique ... J'ai du mal.

[Monsieur23]

Ok.

Donc pour tout n,

Or, pour tous x et y, .

Donc ?

[hgaet]

Donc :
(un) = [e^(pi/2)]^-n

[Monsieur23]

Une suite géométrique est de la forme a^n, ici tu as a^-n.

Il faut que tu mettes le - devant le Pi/2.

Donc ta suite est bien géométrique, de raison Exp(-Pi/2)

[hgaet]

D'accord, et comme 1 > Exp(-Pi/2) > 0 , la suite (un) est strictement décroissante et tend vers 0. C'est ça ?

[Monsieur23]

C'est bien ça !

Bien joué !

Bonne journée à toi.

[hgaet]

Merci bien.:jap:

Bonne journée à toi aussi.