Dérivation d'une équation assez dure!!
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
diabolikus62
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Nov 2008, 15:50
-
 par diabolikus62 » 03 Nov 2008, 20:56
par diabolikus62 » 03 Nov 2008, 20:56
Bonjour à tous !! :we:
Je suis bloqué dans un exercice de DM, pour répondre aux trois dernières questions, qui me semblent faisable, il me faut la dérivée de:
g(x)=x²;)(x²-1)-2
En espérant de l'aide afin de pouvoir finir cet exercice et donc mon DM.
Merci d'avance.
-
aeon
- Membre Relatif
- Messages: 230
- Enregistré le: 24 Oct 2008, 17:00
-
 par aeon » 03 Nov 2008, 21:35
par aeon » 03 Nov 2008, 21:35
Quelle est la dérivée de u*v ?
Quelle est la dérivée de
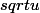
?
Commence le calcul.
-
diabolikus62
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Nov 2008, 15:50
-
 par diabolikus62 » 03 Nov 2008, 22:01
par diabolikus62 » 03 Nov 2008, 22:01
bonjour aeon !
Merci de m'aider.
J'ai trouvé cette réponse :
g'(x)= 2x + [ (2x^3)/(2;)(x²-1) ) ]
avec u= x² u'= 2x v= ;)(x²-1) v'=2x / 2;)(x²-1)
cette dérviation est-elle finie?? Dois-je mettre tout au même dénominateur? Merci aeon
-
aeon
- Membre Relatif
- Messages: 230
- Enregistré le: 24 Oct 2008, 17:00
-
 par aeon » 03 Nov 2008, 22:07
par aeon » 03 Nov 2008, 22:07
Je ne suis pas sûr de ton résultat, parce que je ne suis pas sûr que de bien voir ce qui est sous la racine et ce qui n'y est pas.
Est-ce que g(x) =
}-2)
?
Si oui, ton résultat n'est pas juste.
-
diabolikus62
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Nov 2008, 15:50
-
 par diabolikus62 » 03 Nov 2008, 22:40
par diabolikus62 » 03 Nov 2008, 22:40
Oui c'est bien comme cela qu'est écrite la fonction sur le sujet :hum:
Je ne suis donc pas dans la bonne direction pour réussir a bien cette dérivation selon toi?? :triste:
Alors la je sèche tu peux me mettre sur la voie?? :hein:
Merci encore pour tes réponses.
-
aeon
- Membre Relatif
- Messages: 230
- Enregistré le: 24 Oct 2008, 17:00
-
 par aeon » 03 Nov 2008, 22:46
par aeon » 03 Nov 2008, 22:46
Tu démarres bien
Tu as (presque) écrit : g'(x) = u'(x) * v(x) + u(x) * v'(x)
Sauf qu'il me semble que le v(x) a sauté dans ton calcul.
Et oui, il faut tout mettre au même dénominateur
et ensuite si possible enlever les racines au numérateur.
-
diabolikus62
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Nov 2008, 15:50
-
 par diabolikus62 » 03 Nov 2008, 23:09
par diabolikus62 » 03 Nov 2008, 23:09
Oui excuse moi petite erreur de calcul. Donc cela fait:
g'(x)= 2x;)(x²-1) + (2x^3)/ (2;)(x²-1))
Après il faut mettre tout sa au même dénominateur donc sur 2;)(x²-1).
Mais je n'arrives pas à faire le calcul pour:
2x;)(x²-1) * 2;)(x²-1) si j'ai ce résultat tu me sauve de tout mon DM.
Selon toi quel est le résultat pour cette opération :hein: ?
Je te remercie encore beaucoup :++:
-
aeon
- Membre Relatif
- Messages: 230
- Enregistré le: 24 Oct 2008, 17:00
-
 par aeon » 03 Nov 2008, 23:14
par aeon » 03 Nov 2008, 23:14
2x;)(x²-1) * 2;)(x²-1) = 2x * ;)(x²-1) * 2 * ;)(x²-1)
= 2 * 2x * ;)(x²-1) * ;)(x²-1)
= ...
Tu devrais pouvoir y arriver là.
-
diabolikus62
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Nov 2008, 15:50
-
 par diabolikus62 » 03 Nov 2008, 23:21
par diabolikus62 » 03 Nov 2008, 23:21
Donc si je ne me trompes cela fait:
4x * (x²-1) et donc (4x^3 - 4x) ????
Est-ce cela aeon ? :we:
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 04 Nov 2008, 06:39
par fibonacci » 04 Nov 2008, 06:39
Bonjour;
Si l'on a
=x^2\sqrt{x^2-1^}-2)
=({{u}{v}})^,=u^,v+uv^,=2x\sqrt{x^2-1^}+x^2.\frac{1}{2\sqrt{x^2-1}}.2x)
etc
-
diabolikus62
- Membre Naturel
- Messages: 12
- Enregistré le: 03 Nov 2008, 15:50
-
 par diabolikus62 » 04 Nov 2008, 10:47
par diabolikus62 » 04 Nov 2008, 10:47
Oui d'accord merci pour cette piste.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
