Nombre complexe

[ufuk]

bonjours,

ça fais plus de 3 jours que j'essaie de faire mon dm j'aimerai bien avoir de l'aide SVP.

Voici l'énoncé:

On considere des nombres complexe:
z1 de module 3 et d'argument , z2 de module et d'argument et z3 le conjugué de z2.


Question
1) Ecrire ces nombres complexe sous la forme algébrique .

j'ais fais:
z1= 3 + i, z2= + i, z3= -i

2) représenter les points A1 A2 et A3 d'affixe respectives -3, 1+i et 1-i dans un plan complexe raporté a un repére orthonormal d'origine O.

La je n'ai rien compris

merci de m'aider

[ufuk]

:mur: personne ne peux m'aidé ????

[Rvan]

Bonjour!!!
Voila ce que 'ai trouvé pour le 1):
|Z1|= 3 et arg(Z1)= pi
Donc Z1=3*(cos (pi)+i sin (pi))
Z1=3*(-1+ i 0)
Z1= -3

|Z2|= Racine de 2 et arg ( Z2)=pi/4
Donc Z2 = racine de 2*(cos (pi/4)+i sin ( pi/4))
Z2 = racine de 2 *((racine de 2)/2 + i (racine de 2)/2)
Z2 = 2/2 +i 2/2
Z2 = 1 + i

Comme Z3 est le conjugué de Z2
Z3 = 1-i

Pour le 2) il suffit de construire un repére orthonormal classique d'origine O.
Le point A1 sera donc sur l'axe des abscisses avec A1 (3 ; 0), le point A2 aura pour coordonnées ( 1 ;1 ) et Z3 aura pour coordonnées ( 1 ; -1 ).

Voila, j'espère t'avoir un peu aider!!! :happy2:
by

[ufuk]

merci c'est gentil de m'avoir aidé mais comment avé vous fait pour passé de :
Donc Z2 = racine de 2*(cos (pi/4)+i sin ( pi/4))
Z2 = racine de 2 *((racine de 2)/2 + i (racine de 2)/2)
Z2 = 2/2 +i 2/2

[ufuk]

les i c'est bien sur l'axe des ohrdonne (y)

[Rvan]

Donc Z2 = racine de 2*(cos (pi/4)+i sin ( pi/4))

or tu sais que cos ( pi/4 ) = (racine de 2) /2
et sin (pi / 4) = (racine de 2) /2

Donc tu remplace et ca va te faire

Z2 = racine de 2 * ( (racine de 2 /2) + i (racine de 2)/2 )
tu va distribuer ton racine de 2
D ou Z2= (racine de 2 ) au carré /2 + i (racine de 2 ) au carré / 2
Et Z2 = 2/2 + i 2 /2
Z2 = 1 + i*1
Z2= 1 + i

Sinon oui les i c est bien sur l'axe des ordonnées (y).

[ufuk]

ah ouais lojique je vous remercie

[ufuk]

4)Soit B2 et B3 les symetriques de A2 A3 par rapport a a A1.
a) calculer les formes algébrique et les modules des afixes de B2 e B3.

J'en déduit que la forme algébrique de - B2 c'est: -7 + i
- B3 c'est: -7 +-i

Mais comment je fais pour calculer les modules ???

[Rvan]

Tu peux considérer que B2 symétrique de A2 par rapport à A1 est en fait une translation de vecteur A2A1 qui transforme le point A1 en B2.
Or tu as une formule avec les translations qui te dis que :

Si M et M' ont pour affixe Z et Z'
Si le vecteur w a pour affixe Zw
vecteur MM'= vecteur W
donc Z'-Z= Zw ( car l'affixe du vecteur MM' = Zm' - Zm = Z' - Z
Z'= Z+Zw

Ici ton vecteur w, c est le vecteur A2A1. Son affixe est donné par :
Za1 -Za2 = -3-(1 + i) = -4 -i
Ton Z' c est l affixe du point que tu cherche ici B2
Z , c'est Za1

De la tu remplace :
Zb2 = Za1 + Z ( vecteur A2A1)
ZB2 = -3 -4 -i
Zb2 = -7 -i
Et voila pour Zb2

Pour Zb3 tu reprend la même formula sauf que la :
Ici ton vecteur w, c est le vecteur A3A1. Son affixe est donné par :
Za1 -Za3 = -3-(1 - i) = -4 +i
Ton Z' c est l affixe du point que tu cherche ici B3
Z , c'est Za1

Tu remplace :
Zb3 = Za1 + Z (vecteur A3A1)
Zb3 = -3 -4 +i
Zb3 = -7 +i
Et voila pour Zb3

[Rvan]

Pour les modules tu fais :
|Zb2| = racine ( (-7) au carré + (-1) au carré )
|Zb2| = racine (50)

|Zb3| = racine ( (-7) au carré + 1 au carré )
|Zb3| = racine 50

[ufuk]

hmmmmmmmmmmm je vois comment vousavé fait
sinn j'avais bien raison c'etait bien B2 = -7 + i et B3= -7 +-i ????

derniere question :
-montrer que oB2/oB1 = un nombre entier ?
Comment on peut montrer que c'est un nombre entier alors que quand je mesure je trouve pas un nombre entier ?????

[Rvan]

Pour B2 et B3 regarde mon avant dernier message.

Sinon pour prouver que B2 / B1 est un nombre entier il suffit de calculer.
tu connais B2, tu connais B1.
Divise ...
Et rappel toi qu'on ne peut pas laisser un dénominateur sous forme imaginaire...

[ufuk]

non je me suis trompé je voulé dire OB2/OA2 = un nombre entier
désolé

[Rvan]

Dans ce cas la, il faut que tu calcule les affixes des ces vecteurs.
C'est assez facile étant donné que Zo = 0.
De la tu divise ces affixes...

[ufuk]

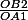
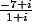
= comme ça ???

[Rvan]

Presque Zb2 = -7-i
Donc ca te fait (-7-i) / (1+i) et de la tu calcules et n'oublie pas : pas de nombre imaginaire au dénominateur.
Tu dois avoir un moyen dans ton cours de résoudre ce problème.

[Rvan]

C'est OB2/OA2 ou OB2/OA1 comme dans ton dernier message?

[ufuk]

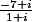
mais nn OB2 c'est et ensuite on fais le conjugué nn ?

[Rvan]

non non

"Tu peux considérer que B2 symétrique de A2 par rapport à A1 est en fait une translation de vecteur A2A1 qui transforme le point A1 en B2.
Or tu as une formule avec les translations qui te dis que :

Si M et M' ont pour affixe Z et Z'
Si le vecteur w a pour affixe Zw
vecteur MM'= vecteur W
donc Z'-Z= Zw ( car l'affixe du vecteur MM' = Zm' - Zm = Z' - Z
Z'= Z+Zw

Ici ton vecteur w, c est le vecteur A2A1. Son affixe est donné par :
Za1 -Za2 = -3-(1 + i) = -4 -i
Ton Z' c est l affixe du point que tu cherche ici B2
Z , c'est Za1

De la tu remplace :
Zb2 = Za1 + Z ( vecteur A2A1)
ZB2 = -3 -4 -i
Zb2 = -7 -i
Et voila pour Zb2"

Donc Zb2 = -7 -i

Ensuite je pensai qu'en faisant le conjugué on pourrai démontrer que ce nombre été un nombre entier mais ça ne marche pas apparemment et je n ai pas d'autres idées pour le prouver...
Tu es sur qu'il faut bien prouver que c'est un entier?

[ufuk]

woah votre théoreme j'ai rien compris mais sinn oui il faut trouvé un nombre entier