Intégrales-Intégrations par parties
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 01 Nov 2008, 13:59
par Dimitri22 » 01 Nov 2008, 13:59
Bonjour,
je bloque à une question de mon DM:
Avec une intégration par parties soigneusement justifiée, montrez que K(x)-3L(x) est négligeable devant (e^(x))/(x²) lorsque x tend vers +infini.
Avec K(x) est l'intégrale de 1 à x de ((e^(t))/(t^3))dt
L(x) est l'intégrale de 1 à x de ((e^(t))/(t^4))dt
Je sais que par exemple f est négligeable devant g au voisinage de +infini si lim (f(x)/g(x))=0 quand x tend vers +infini.
Est-ce que je dois utiliser ceci? Parce qu'on ne connait pas l'expression des fonctions L et K. Et quelle intégraion par partie puis-je utiliser?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 01 Nov 2008, 15:23
par tize » 01 Nov 2008, 15:23
Bonjour,
=\int_1^x\frac{e^t}{t^3}dt)
pose l'IPP avec
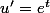
et
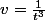
, tu peux ensuite écrire K(x) en fonction d'un terme en x et de 3L(x), après reste à faire ce que tu as écris dans ton message : montrer que le quotient tend vers 0...
-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 01 Nov 2008, 16:15
par Dimitri22 » 01 Nov 2008, 16:15
merci beaucoup :)
-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 01 Nov 2008, 16:56
par Dimitri22 » 01 Nov 2008, 16:56
Ok donc je viens de montrer que K(x)-3L(x) est négligable devant (e^(x))/(x²) quand x tend vers +infini.
Mais comment je peux montrer que L(x) est négligeable devant (e^(x))/(x²) lorsque x tend vers +infini?
Je ne vois pas trop s'il faut s'aider de la réponde précédente ou pas.
-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 01 Nov 2008, 23:58
par Dimitri22 » 01 Nov 2008, 23:58
Personne n'a une petite piste?
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 02 Nov 2008, 09:12
par miikou » 02 Nov 2008, 09:12
et bien elle f est negligable devant g si f/g -> 0
donc ln(x) / ( e^x / x² ) = x²*ln(x)*e^-x -> 0 ?
<=> e^( 2ln(x) - x)*ln(x) -> 0 ?
or ln(x) < x
donc 2ln(x) - x < ln(x)
par croissance de exp on a e^( 2ln(x) - x)*ln(x) < e^(lnx))*ln(x) = ln(x)/x qui tend bien vers 0 par croissance comparée, on conclus avec le th des gendarmes ;)
-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 02 Nov 2008, 18:28
par Dimitri22 » 02 Nov 2008, 18:28
Pourquoi tu as pris lnx?
L(x) c'est pas ln(x) ^^ c'est une intégrale
L(x) est l'intégrale de 1 à x de ((e^(t))/(t^4))dt
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 02 Nov 2008, 19:37
par tize » 02 Nov 2008, 19:37
Salut,
tu peux étudier la fonction

, elle est continue sur
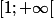
, strictement croissante à partir d'un certain point et tend vers

, on peut donc dire qu'il existe

tq
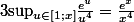
dès que

et donc :
\leq \frac{e^x}{x^4}\(x-1\))
dès que

, reste à diviser par

pour obtenir ce que tu cherches.
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 02 Nov 2008, 21:54
par miikou » 02 Nov 2008, 21:54
Dimitri22 a écrit:Pourquoi tu as pris lnx?
L(x) c'est pas ln(x) ^^ c'est une intégrale
L(x) est l'intégrale de 1 à x de ((e^(t))/(t^4))dt
mdr c'est leffet lendemain de boite ( comprend de cuite :p )
-
Dimitri22
- Membre Naturel
- Messages: 18
- Enregistré le: 01 Nov 2008, 13:50
-
 par Dimitri22 » 03 Nov 2008, 00:03
par Dimitri22 » 03 Nov 2008, 00:03
Merci beaucoup!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 03 Nov 2008, 00:10
par tize » 03 Nov 2008, 00:10
De rien :we: mais le travail n'est pas fini, il y a des choses à éclaircir un peu, comme l'existence de cette constante C...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
