DM base orthonormée / produit scalaire

[romulus001]

h(xP,Q)=h(P,xQ)

Comme est de degrés n, h(,Q)=0 si deg(Q)<n-2<n=deg()

(de degrés n) peut se décomposer comme étant une somme des avec i qui va de 1 jusqu'à n

[Purrace]

Tu en est à quelle question?

[Doraki]

h(xP,Q) = h(P,xQ), oui.

romulus, il y a des liens logiques entre mes questions.
Je te pose pas une question pour que tu oublies le résultat tout de suite après

Tu as dit :

h(xP(n-1),Q)=0 si deg(Q)<n-2<n = deg(xP(n-1))

Donc apparemment, h(A,B) ça vaut 0 dès que d°A < d°B ou que d°B < d°A ?
Tu crois pas que si j'avais pu dire "si d°Q < n" au lieu de "d°Q < n-2" je l'aurais fait ?

Le seul moyen que tu as de montrer qu'un produit scalaire h(A,B) est nul,
c'est d'utiliser le fait que (Pn) est une base orthonormée, c'est tout.
Et plus simplement, le résultat de la question 1e)

[romulus001]

Purrace--> question 2)a)

Doraki--> j'ai voulu me servir de la question e), et je pensais que était un à cause du degrés, mais en réalité, c'est un faux .

Vous me dites qu'il y a des liens logiques, mais je ne vois pas de rapprochement avec ce qui est demandé.
Concernant h(xP(n-1),Q), je dis que c'est h(P(n-1),xQ)=h(P(n-1), somme(ai*x^(i+1), i de 0 à n-2))=somme( ai*h(P(n-1),x^(i+1) ))=0

[Doraki]

Comme xQ est de degré < n-1, la question 1e dit que h(P(n-1),xQ) = 0 oui.

Maintenant, comme les Pn sont une base orthonormée, tout polynôme P de degré <= n se décompose comme ça :
P = h(P,P0)P0 + h(P,P1)P1 + ... + h(P,Pn)Pn.

Pour P = xP(n-1), il y a quoi comme termes non nuls dans cette décomposition ?
A partir de là il suffit juste de tourner cette égalité pour avoir Pn en fonction du reste pour finir la question.

[romulus001]

Maintenant, comme les Pn sont une base orthonormée, tout polynôme P de degré n ou +infini) (x/en)en avec {en,n} base canonique et (./.) produit scalaire

Pour P = xP(n-1), il y a quoi comme termes non nuls dans cette décomposition ?
A partir de là il suffit juste de tourner cette égalité pour avoir Pn en fonction du reste pour finir la question.

Seuls les 3 derniers termes de la somme ne sont pas nuls: h(P(n-1),xP(n-2)), h(P(n-1),xP(n-1)) et h(P(n-1),xPn)

donc x=h(,x)+h(,x)+h(,x)

donc h(,x)=[ x- h(,x) ] - h(,x)

Ainsi, =[ x+ ]+

Par identification avec le début du 2)a)
=, = et =

[Doraki]

Est-ce que c'est toujours vrai?
Dans mon cours, on avait dit qu'un vecteur x s'écrivait comme somme(i=0 --> n ou +infini) (x/en)en avec {en,n} base canonique et (./.) produit scalaire

Ben.. c'est pas ce que dit ton cours, justement ?

Par identification avec le début du 2)a)
=, = et =

non il suffit juste de dire "On a l'équation recherchée en prenant an = ... bn = ... et cn = ..."
Si tu dis "par identification" ça suppose que t'aies déjà montré qu'il existait an, bn, cn tels qu'on ait ça, et qu'en plus tu aies montré qu'une telle décomposition était unique.

[romulus001]

Ben.. c'est pas ce que dit ton cours, justement ?

Je pensais que ce n'était pas pareil, vu que {Pn,n} n'est pas une base canonique, mais les {X^n,n} oui, puisqu'on est dans les polynômes...

non il suffit juste de dire "On a l'équation recherchée en prenant an = ... bn = ... et cn = ..."
Si tu dis "par identification" ça suppose que t'aies déjà montré qu'il existait an, bn, cn tels qu'on ait ça, et qu'en plus tu aies montré qu'une telle décomposition était unique.

oui, oui, c'est vrai, une fois de plus, j'ai parlé un peu trop vite :ptdr:

Pour la valeur des an, il faut vérifier que h(,xPn)=

D'après mes notations dans 1)b) et celle du texte, =

Il faut maintenant vérifier que h(,xPn)=1/gamma(n)

Maintenant, dans l'intégrale, je ne met plus la fonction w pour aller plus vite (vu qu'elle ne nous apporte pas grand chose), ni le dx, ni les bornes de l'intégrale

=-

donc = xPn(-)=- =-

là, je bloque, j'ai l'impression qu'il va falloir s'y prendre autrement :mur:

[Doraki]

Dans la relation Pn = (an x + bn)P(n-1) + cn P(n-2),
quel est le coefficient de X^n ?

[romulus001]

:marteau:
Encore une fois, je n'ai pas vu le côté "astucieux" du problème...

Si on regarde Pn à lui-seul, son coeff dominant est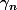
Mais si on regarde Pn comme (an*x+bn)P(n-1)+cn*P(n-2), son ceff dominant est 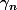an*
=an* et donc
an=/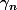

edit: pour cn, qui vaut -h(P(n-1),xP(n-2))/h(P(n-1),xP(n)), on reconnait le an(=1/h(...)), et donc cn=-an*h(P(n-1),xP(n-2))=-an*h(P(n-2),xP(n-1)=-an/a(n-1)

[romulus001]

j'ai su faire la question 2)c), j'ai fait par récurrence, ça passe tout seul :we:

Par contre, pour les questions d) et e), je ne sais même pas comment faire pour démarrer...
Pour le d), poser =, mais je ne sais pas quoi faire de plus ...

[Doraki]

pour le d faut juste dire que f'(x) c'est la limite de (f(x)-f(y))/(x-y) quand y tend vers x.

[romulus001]

Si je comprends bien, je dis que
=f'(x)-f'(y)=limite [y->x de (f(x)-f(y))/(x-y)] - limite [x->y de (f(y)-f(x))/(y-x)]


Pour le e), je ne vois pas le coté "en déduire"...

Pour le 3)a), je peux dire que h(Pi,Pj)=0 ou 1, car {Pn,n} base orthonormée?
Pour finir, que tout polynôme P s'écrit somme(i=0 -> +infini) h(P,Pi)Pi , qui est continu, donc mesurable, donc h(P,P)=< + infini

3)b) j'oublie w, dx et les bornes de l'intégrale pour simplifier l'écriture.
P(x)Kn(x,y)=P(x)Pi(x)Pi(y)= P(x)Pi(x) * Pi(y)=\sum_{i=0}^n[/TEX] h(P,Pi) Pi(y) =P(y)

Kn(x,y)= 1*Kn(x,y)=h(1,Kn(.,y))=1

[Doraki]

Si je comprends bien, je dis que
=f'(x)-f'(y)=limite [y->x de (f(x)-f(y))/(x-y)] - limite [x->y de (f(y)-f(x))/(y-x)]

??? c'est quoi ton f ?
Je disais juste de remplacer les P' par des limites.

[romulus001]

f(x)=
f(y)=

donc P=limite [y->x de (f(x)-f(y))/(x-y)] - limite [x->y de (f(y)-f(x))/(y-x)]
c'est bien ça?

[Doraki]

J'ai rien compris à ta fonction f.
Ca vaut combien f(17) ?

Et puis pourquoi tu parles de y à la base si tu veux calculer P'(n+1)(x)Pn(x) - P(n+1)(x)P'n(x) de manière à obtenir un lim(y->x) (truc avec x et y)/(x-y).

[romulus001]

je n'avais compris que toute l'expression était avec une seule et même variable, je faisais le rapprochement avec l'expression de la question 2)c)

je viens d'avoir un résultat, mais je ne sais pas si ça convient à la question, puisqu'on demande "une" expression de P'(n+1)Pn-P'nP(n+1)

j'ai finalement posé f(x,y)=( P(n+1)(x)Pn(y)-P(n+1)(y)Pn(x) )/(x-y)

Pour trouver la limite quand y--> x, j'utilise le théorème de l'Hospital, en dévirant par rapport à y, et j'obtiens P'(n+1)Pn(x)-P'n(x)P(n+1)(x)

[Doraki]

ça marche oui mais j'aime pas la règle de l'hopital.
Si tu pars du résultat et que tu fais apparaitre les dérivées explicitement, t'obtiens une preuve plus facile :

(P(n+1)(x)Pn(y)-P(n+1)(y)Pn(x))/(x-y)
= (P(n+1)(x)Pn(y)-P(n+1)(y)Pn(y))/(x-y) - (P(n+1)(y)Pn(x)-P(n+1)(y)Pn(y))/(x-y)
= Pn(y) * (P(n+1)(x)-P(n+1)(y))/(x-y) - P(n+1)(y) * (Pn(x)-Pn(y))/(x-y)

Donc en faisant tendre y vers x, la limite devient bien Pn(x) * P'(n+1)(x) - P(n+1)(x) * P'n(x).

Pour la suite, je suppose que tu dois montrer que Kn(x,x) ne peut pas être nul, peut-être qu'il est strictement positif.

[romulus001]

c'est bizarre, quand c'est simple, je prends toujours un mauvais chemin!!


a(n+1)Kn(x,x)=P'(n+1)Pn(x)-P'n(x)P(n+1)(x)

Si on suppose que Pn(x)=0,on a

a(n+1)Kn(x,x)=somme(i=0 -> n) Pi(x)²=-P'n(x)P(n+1)(x)>0 (on ne peut pas avoir =0 car P0(x)<>0) et donc P(n+1)(x) <> 0

On montre de même que P(n+1)(x)<>0

[romulus001]

Concernant la question où il faut montrer qu'entre 2 racines de P(n+1) consécutives, il y a 1 racine de Pn, je dirais qu'il faut se placer sur un intervalle [r1,r2] où r1 et r2 sont 2 racines consécutives de P(n+1), mais je n'arrive pas à construire une fonction Fn qui mélangerait Pn et P(n+1) et que Fn(r1)Fn(r2)<0 :triste: