Inégalité
Olympiades mathématiques, énigmes et défis
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 12 Déc 2005, 20:56
par yos » 12 Déc 2005, 20:56
Pas bien dur :
G isobarycentre de A,B,C,D.
GA+GB+GC+GD<=AB+BC+CD+DA
-
altusi
- Membre Naturel
- Messages: 20
- Enregistré le: 22 Aoû 2005, 21:06
-
 par altusi » 16 Déc 2005, 11:25
par altusi » 16 Déc 2005, 11:25
sympa ton exos:
G est l'isobarycentre de a,b,c,d donc:
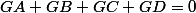
(avec vecteurs),ce qui donne en faisant intervenir les points A,B,C,D:

en procedant de meme pour les 4 points,on obtient:
|
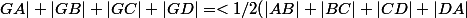 +1/2(|BD|+|AC|)=<1/2(|AB|+|BC|+|CD|+|DA|) +1/2(|AB|+|BC|+|CD|+|DA|))
d'ou le resultat§
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Déc 2005, 13:14
par yos » 16 Déc 2005, 13:14
Bien vu!
Cela reste vrai en remplaçant G par un point M d'un segment bimédiant (i.e. appartenant à un segment [IJ] joignant les milieux de [AB] et [CD] par exemple).
-
altusi
- Membre Naturel
- Messages: 20
- Enregistré le: 22 Aoû 2005, 21:06
-
 par altusi » 16 Déc 2005, 17:10
par altusi » 16 Déc 2005, 17:10
peut etre oui ,puisqu'on pourrait faire une petite generalisation en mettant G le barycentre de {(A,x),(B,y),(C,z),(D,w)} :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
