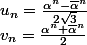On définit la suite
Montrer que pour tout n,
Un problème amusant et intéressant mais posé exprès de la pire manière possible, et je ne me verrais certainement pas le donner à des lycéens.
Une suite d'entiers ?
11 messages
- Page 1 sur 1
Une suite d'entiers ?
par Doraki » 07 Oct 2008, 12:44
J'ai trouvé ça dans des vieilles annales d'olympiades
On définit la suite
par récurrence par :
.
Montrer que pour tout n, est un entier.
Un problème amusant et intéressant mais posé exprès de la pire manière possible, et je ne me verrais certainement pas le donner à des lycéens.
On définit la suite
Montrer que pour tout n,
Un problème amusant et intéressant mais posé exprès de la pire manière possible, et je ne me verrais certainement pas le donner à des lycéens.
par nodgim » 07 Oct 2008, 17:30
Il suffit de montrer que u(n+1)=4un-u(n-1). :happy2:
En effet, on retrouve que 3un²+1=(2un-u(n+1))².
Pas simple, et puis je reste sur ma faim, car j'ai trouvé par tâtonnement, sans en comprendre la substantifique moelle :doh:
J'espère qu'il y a quelque chose de plus propre..
En effet, on retrouve que 3un²+1=(2un-u(n+1))².
Pas simple, et puis je reste sur ma faim, car j'ai trouvé par tâtonnement, sans en comprendre la substantifique moelle :doh:
J'espère qu'il y a quelque chose de plus propre..
par Zweig » 07 Oct 2008, 17:36
Salut,
est entier si et seulement si il existe un entier 
tel que 
pour tout 
. On reconnait ici une équation de Pell-Fermat. La solution minimale est  = (2,1))
, donc l'ensemble des solutions de est donné par la formule :
^{n}-\left(2-\sqrt{3}\right)^{n}}{2\sqrt{3}})
Il "suffit" alors de montrer par récurrence que vérifie la relation de récurrence.
Il "suffit" alors de montrer par récurrence que
par Zweig » 07 Oct 2008, 18:54
Salut,
est entier si et seulement si il existe un entier tel que pour tout . On reconnait ici une équation de Pell-Fermat. La solution minimale est , donc l'ensemble des solutions de est donné par la formule :
Il "suffit" alors de montrer par récurrence que vérifie la relation de récurrence.
Soit
la proposition suivante : "
, "
est clairement vraie.
On se fixe un entier
tel que 
soit vraie. Montrons qu'alors 
est vraie aussi :
^{k}-\left(2-\sqrt{3}\right)^{k}\right]}{2\sqrt{3}} + \sqrt{\frac{\left[\left(2+\sqrt{3}\right)^{k}-\left(2-\sqrt{3}\right)^{k}\right]^{2}}{4}+1})
^{k}-\left(2-\sqrt{3}\right)^{k}\right]}{2\sqrt{3}} + \sqrt{\frac{\left(2+\sqrt{3}\right)^{2k}-2\left[\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)\right]^{k}+\left(2-\sqrt{3}\right)^{2k}}{4}+1})
^{k}-\left(2-\sqrt{3}\right)^{k}\right]}{2\sqrt{3}} + \sqrt{\frac{\left(2+\sqrt{3}\right)^{2k}+2+\left(2-\sqrt{3}\right)^{2k}}{4}})
^{k}-\left(2-\sqrt{3}\right)^{k}\right]}{2\sqrt{3}} + \sqrt{\left[\frac{\left(2+\sqrt{3}\right)^{k}+\left(2-\sqrt{3}\right)^{k}}{2}\right]^{2}})
^{k}-\left(2-\sqrt{3}\right)^{k}\right]}{2\sqrt{3}} + \frac{\left(2+\sqrt{3}\right)^{k}+\left(2-\sqrt{3}\right)^{k}}{2})
^{k}\left(2+\sqrt{3} \right )-\left(2-\sqrt{3}\right)^{k}\left(2-\sqrt{3}\right)}{2\sqrt{3}})
^{k+1}-\left(2-\sqrt{3}\right)^{k+1}}{2\sqrt{3}})
Donc est vraie. Par suite, pour tout 
, on a , qui est bien entier d'après le binôme de Newton.
Il "suffit" alors de montrer par récurrence que
Soit
On se fixe un entier
Donc
par Doraki » 07 Oct 2008, 20:03
nodgim :
Oui c'est une bonne relation de récurrence, note que les racines de X²-4X+1 sont
.
Et on peut prouver que 3un²+1=(2un-u(n+1))² par récurrence, en effet.
Zweig :
Une bonne formule pour un et un calcul un tout petit peu long.
Le point principal étant que(2-\sqrt3) = 1)
(on le voit plus clairement que dans la preuve de nodgim)
En trigonométrie tu préfères les formules d'Euler ou la formule de de Moivre ?
Je sais pas exactement d'où c'était, pour ça faudrait que j'aille vérifier dans le bouquin et j'y penserai jamais.
Oui c'est une bonne relation de récurrence, note que les racines de X²-4X+1 sont
Et on peut prouver que 3un²+1=(2un-u(n+1))² par récurrence, en effet.
Zweig :
Une bonne formule pour un et un calcul un tout petit peu long.
Le point principal étant que
En trigonométrie tu préfères les formules d'Euler ou la formule de de Moivre ?
Je sais pas exactement d'où c'était, pour ça faudrait que j'aille vérifier dans le bouquin et j'y penserai jamais.
par Zweig » 07 Oct 2008, 20:07
En trigonométrie tu préfères les formules d'Euler ou la formule de de Moivre ?
Pourquoi cette question ? :hein:
J'ai volontairement détaillé les calculs pour ceux qui me liront comprennent :++:
par Doraki » 07 Oct 2008, 20:36
Parceque ta formule générale pour u_n est de type formule d'euler comme dans sin x = (e^ix - e^-ix)/2i.
Et je préfère de loin e^ix = cos x + i sin x je trouve que ça explique plus clairement le lien entre cos sin et exp.
Et je préfère de loin e^ix = cos x + i sin x je trouve que ça explique plus clairement le lien entre cos sin et exp.
par Doraki » 20 Oct 2008, 09:59
Ma solution :
Tout est basé sur)
.
Soient
et les coordonnées (entières) de 
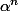
dans la base )
de )
. :
^n = v_n + u_n \sqrt 3)
On a facilement les relations de récurrence
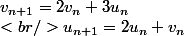
est de norme 1 : (2-\sqrt3) = v_1^2 - 3u_1^2 = 1)
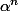
La norme est multiplicative, et donc vaut 1 aussi, ce qui veut dire exactement que 
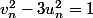
Et si vous connaissez pas la norme, c'est une relation qui se montre immédiatement par récurrence.
La relation de récurrence d'ordre 2 correspond au polynôme minimal de, à savoir X²-4X +1.
On a
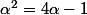
. En multipliant ça par 
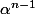
et en l'écrivant en termes de coordonnées, on voit alors que et vérifient toutes les deux cette relation d'ordre deux 
.
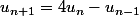
Les formules générale pour et sont obtenues de la même façon que les formules d'Euler en trigonométrie :
Tout est basé sur
Soient
On a facilement les relations de récurrence
La norme est multiplicative, et donc
Et si vous connaissez pas la norme, c'est une relation qui se montre immédiatement par récurrence.
La relation de récurrence d'ordre 2 correspond au polynôme minimal de
On a
Les formules générale pour
par ThSQ » 20 Oct 2008, 18:04
Doraki a écrit:Ma solution
C'est un peu marteau-pilonnesque non ?
Avec des manips élémentaires on a :
et donc aussi
et donc en soustrayant (tous diff.) :
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :