Bonjour,
On considère l'application f de R² dans R^4 donnée par
f(a,b)=(cosa,sina,cosb,sinb) et il faut prouver que f fournit un difféomorphisme g de R²/(2piZ)² (Z=entier) sur f(R²). Mais je ne vois pas comment démarrer donc toute proposition est bienvenue. :we:
Variétés différentielles
4 messages
- Page 1 sur 1
par Nightmare » 23 Oct 2008, 23:25
Salut :happy3:
Eh bien commence par revenir à la définition d'un difféomorphisme non? :lol3:
Eh bien commence par revenir à la définition d'un difféomorphisme non? :lol3:
par mathelot » 24 Oct 2008, 09:43
Bjr,
Soit U le cercle unité du plan complexe.
f s'écrit plus simplement
 \rightarrow (e^{ia},e^{ib}))
f est donc un morphisme de groupes, continue.
Par passage au quotient (la topologie quotient est faite pour cela)
g est un isomorphisme de groupes (bijectif, continue).
g est une application ouverte (l'image d'un ouvert est un ouvert)
essentiellement car , en passant au complémentaire,
l'image d'un compact est compacte donc fermée dans l'ensemble d'arrivée.
g est donc un homéomorphisme.
Ensuite , on différentie:
(h_1,h_2)=(ie^{ia}h_1,ie^{ib}h_2))
la différentielle est donc une application
-linéaire
injective sur l'espace tangent de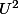
au point )
l'espace tangent de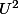 en un point est tout simplement constitué des directions des deux tangentes aux deux cercles.
La différentielle est donc bijective, puisque l'espace tangent de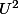 en un point, est de dimension 2 sur
résultat des courses,)
est une bijection de 
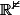sur l'espace tangent à } (U^2))
g est donc un difféomorphisme, d'après un thm de calcul différentiel.
PS: on écrit pour )
par abus d'écriture, la valeur des exponentielles ne dépend que des classes de a et b, modulo
Soit U le cercle unité du plan complexe.
f s'écrit plus simplement
f est donc un morphisme de groupes, continue.
Par passage au quotient (la topologie quotient est faite pour cela)
g est un isomorphisme de groupes (bijectif, continue).
g est une application ouverte (l'image d'un ouvert est un ouvert)
essentiellement car , en passant au complémentaire,
l'image d'un compact est compacte donc fermée dans l'ensemble d'arrivée.
g est donc un homéomorphisme.
Ensuite , on différentie:
la différentielle est donc une application
injective sur l'espace tangent de
l'espace tangent de
La différentielle est donc bijective, puisque l'espace tangent de
résultat des courses,
g est donc un difféomorphisme, d'après un thm de calcul différentiel.
PS: on écrit
par abus d'écriture, la valeur des exponentielles ne dépend que des classes de a et b, modulo
par cyclique » 24 Oct 2008, 15:57
merci pour ta réponse. J'ai trouvé cet exercice sur internet mais je ne connaissais pas encore les notions d'espace tangent...(j'ai vu cela aujourd'hui)
Je ne pensais pas que ces notions étaient indispensables pour la résolution. :lol5:
Je ne pensais pas que ces notions étaient indispensables pour la résolution. :lol5:
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :