Variations de f , term S

[hpauline]

bonsoir , je n'arrive pas à trouver le signe de f ' (x) sur ]1 ; +infini [
(duquel je dois déduire le tableau de variation de f )
avec f(x) =

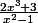
pourriez vous m'aider ? c'est assez urgent , et le reste de l'exercice dépend de cette question , merci de votre aide !

[le_fabien]

Bonsoir,
as tu calculé f'(x) , peux tu la donner ?

[Le Chaton]

Bonsoir,

il suffit d'appliquer la dérivé d'un quotient.
(U/V)'=...
Et de trouver le signe du numérateur...

[le_fabien]

Bonsoir,

il suffit d'appliquer la dérivé d'un quotient.
(U/V)'=...
Et de trouver le signe du numérateur...

C'est certain mais hpauline nous dit qu'elle(il) n'arrive pas à determiner le signe de f' , cela veut dire qu'elle(il) a calculé cette dérivée. :we:

[Le Chaton]

Effectivement ... mais ne l'ayant pas fait moi même je ne savais pas si la difficulté était de trouver f' ou bien son signe. Apparemment c'est son signe

[hpauline]

la dérivée est , d'après mes calculs (...) la suivante :
f ' (x) =

[le_fabien]

J'ai la même dérivée , maintenant il faut factoriser par 2x

[hpauline]

merci , je vais essayer de continuer !

[hpauline]

une autre question me pose problème :

je dois démontrer que la droide D d'équation y = x-2 est asymtote à Cf en + infini

soit f(x) =

la formule est la suivante :

[hpauline]

(le signe sous limite signifie , tend vers + infini )

[le_fabien]

Il faut transformer f(x)-(x-2) grâce à l'expression conjuguée

[hpauline]

ça me revient , merci

[oscar]

Bonsoir


lim[ V( x² - 4x-5) -(x-2)] si x--> +oo
Au départ :oo-oo

lim (x²-4x-5 - x² + 4x - 4)/[(v(x²-4x-5) + (x-2)] ---> 0