[résolue] (Nouvelle) demande de confirmation de la divergenc

[Yavzz]

Hier soir, j'avais déjà posé une question du même type,
Pour a (< ou =) 0,je veux juste savoir si diverge bel et bien, en utilisant des équivalents.

J'espère ne pas aller à l'encontre des règles du forum en posant 2 posts à la suite (si c'est le cas, je supprimerais le post...).

Merci d'avance.

[tize]

Bonjour,
pour revenir sur les trucs classiques tu peux poser le changement de variable a-u=t

[Yavzz]

Justement, j'ai un peu de mal dans les bornes de l'intégrale avec les changements de variables, et à finaliser le tout.

Est-ce que je peux écrire mon raisonnement pour voir s'il n'y pas d'incohérence?

[tize]

Oui oui, tu peux

[Yavzz]

En posant, t = a - u, on a =

Ensuite, est négligeable devant 1/t en 0. { je doute de la véracité de ce passage}
...
...
On en conclue que notre intégrale n'existe pas.

[tize]

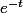
tend vers quoi en 0 ? Donc à quoi ?

[Yavzz]

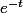
tend vers quoi en 0 ? Donc à quoi ?

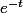
tend vers 1 en 0,
donc
....
Merci.

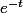
Mais en fait, hier soir dans mon post j'avais proposé la même chose en faisant , on m'a dit que c'était une erreur de faire tendre le t vers 0 dans vers 1 et de ne pas le faire dans 1/t.

Il me semblait bien que j'avais raison hier soir sur mon post, c'est pour ça que je n'étais plus trop sûr pour cette intégrale, en tout cas merci beaucoup. :happy2:

[tize]

Je ne sais pas ce qu'il s'est dit dans ton post hier mais en tout cas, on a évidemment bien

[Yavzz]

Merci beaucoup....