Prouver une inégalité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
HH.What?
- Membre Naturel
- Messages: 26
- Enregistré le: 06 Sep 2008, 11:16
-
 par HH.What? » 18 Oct 2008, 18:37
par HH.What? » 18 Oct 2008, 18:37
Bonsoir, comment montreriez vous que
\displaystyle \leq \frac{x^{2}}{2})
?
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 18 Oct 2008, 18:52
par Skullkid » 18 Oct 2008, 18:52
Bonsoir, tu peux appliquer l'inégalité de Taylor-Lagrange si tu la connais, ou sinon tu peux étudier la fonction
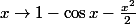
.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 18 Oct 2008, 20:06
par leon1789 » 18 Oct 2008, 20:06
tu peux aussi dériver deux fois (sans faire de Taylor) et étudier le signe des deux dérivées !
-
mathelot
 par mathelot » 19 Oct 2008, 07:06
par mathelot » 19 Oct 2008, 07:06
leon1789 a écrit:tu peux aussi dériver deux fois (sans faire de Taylor) et étudier le signe des deux dérivées !
bah oui,
si x>0, on intégre sur [0;x] , l'inégalité:
 \leq t)
puis, le résultat reste valable pour

car les fonctions sont paires.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
