Règle de l'hôpital
56 messages
- Page 1 sur 3 - 1, 2, 3
Règle de l'hôpital
Bonjour
J'ai un probleme en probabilité, je doit calculer la fonction des moments et j'ai besoin pour cela de la règle de l'hôpital. cependant je n'ai aucun souvenir qu'on me l'aie montré dans les cours de dérivation et je n'ai trouvé aucune documentation capable de me l'expliquer clairement. si quelqu'un pouvait m'aider en m'expliquant le principe ca serrait très apprécié.
J'ai un probleme en probabilité, je doit calculer la fonction des moments et j'ai besoin pour cela de la règle de l'hôpital. cependant je n'ai aucun souvenir qu'on me l'aie montré dans les cours de dérivation et je n'ai trouvé aucune documentation capable de me l'expliquer clairement. si quelqu'un pouvait m'aider en m'expliquant le principe ca serrait très apprécié.
Si une règle ne sert qu'à encombrer l'esprit d'un élève ou d'un étudiant elle est inutile voire néfaste ( ce n'est pas de l'humour ) . Cette règle peut à la rigueur être vue en exercice ( et encore ) , le mieux serait de l'oublier . Ou alors qu'on me montre un seul exemple où elle sert à quelque chose .
Imod
Imod
Imod tu me sembles bien définitif...
nuage illustre l'utilité de la règle avec un bel exemple...
Dans tous les cas où on se retrouve avec une forme indéterminée du type 0/0 ou inf/inf, elle est utile! C'est rapide et efficace...
J'aimerais bien qu'on m'explique ce que le monde a contre cette règle, ça me semble bien arbitraire.
Il faut l'utiliser avec précaution certes, il n'empêche qu'elle est valide.
Au Québec elle est enseigné, en France il me semble que non, à moins que ça ait changé ces derniers temps.
Stef
nuage illustre l'utilité de la règle avec un bel exemple...
Dans tous les cas où on se retrouve avec une forme indéterminée du type 0/0 ou inf/inf, elle est utile! C'est rapide et efficace...
J'aimerais bien qu'on m'explique ce que le monde a contre cette règle, ça me semble bien arbitraire.
Il faut l'utiliser avec précaution certes, il n'empêche qu'elle est valide.
Au Québec elle est enseigné, en France il me semble que non, à moins que ça ait changé ces derniers temps.
Stef
re,
pour comprendre la règle de l'Hospital,il faut être un peu malade. :++:
soit f et g de classe continuement dérivables.
continuement dérivables.
avec
=lim_{x \rightarrow 0} g(x)=0)
Le théorème des accroissements finis donne:
=f(x)-f(0)=x f'(\xi)) pour un certain
pour un certain 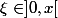
d'où}{x} = lim_{\xi \rightarrow 0} f'(\xi))
d'où}{g(x)} = lim_{x \rightarrow 0} \frac{(\frac{f(x)}{x})}{(\frac{g(x)}{x})}= \frac{lim_{x \rightarrow 0} f'(x)}{lim_{x \rightarrow 0} g'(x)})
C'est un des Bernoulli , l'inventeur de ce théorème. Comme Bernoulli était fauché, il donnait , moyennant finance, des cours particuliers au riche marquis de l'Hospital, et a fini par lui vendre son théorème.
Cette règle était utilisée dans les années 1970 en classe de Terminale française, quand le théorème des accroissements finis était au programme mais pas les développements limités.
pour comprendre la règle de l'Hospital,il faut être un peu malade. :++:
soit f et g de classe
avec
Le théorème des accroissements finis donne:
d'où
d'où
C'est un des Bernoulli , l'inventeur de ce théorème. Comme Bernoulli était fauché, il donnait , moyennant finance, des cours particuliers au riche marquis de l'Hospital, et a fini par lui vendre son théorème.
Cette règle était utilisée dans les années 1970 en classe de Terminale française, quand le théorème des accroissements finis était au programme mais pas les développements limités.
PrépaQuébec a écrit:Imod tu me sembles bien définitif...
nuage illustre l'utilité de la règle avec un bel exemple...
Dans tous les cas où on se retrouve avec une forme indéterminée du type 0/0 ou inf/inf, elle est utile! C'est rapide et efficace...
Stef
lim(x/x) j'espère que c'est une blague !
Cette règle est un artifice qui perd tout intérêt dès que l'on connait les développements limités alors pourquoi perdre son temps avec ?
Imod
Bof, moi j'aime bien cette règle de l'Hospital...
Elle permet de lever très rapidement des indéterminations qui prennent du temps sinon... Ca énerve d'ailleurs bien les profs quand on l'utilise : il voudrait qu'on lève des indéterminations autrement, de façon plus compliquée, mais bon, on préfère faire simple...
Elle permet de lever très rapidement des indéterminations qui prennent du temps sinon... Ca énerve d'ailleurs bien les profs quand on l'utilise : il voudrait qu'on lève des indéterminations autrement, de façon plus compliquée, mais bon, on préfère faire simple...
Comme Imod, je ne vois pas en quoi  est un "bel exemple", c'est le genre de fonction qu'on utilise comme exemple pour introduire le prolongement par continuité, justement parce qu'une telle limite est triviale...
est un "bel exemple", c'est le genre de fonction qu'on utilise comme exemple pour introduire le prolongement par continuité, justement parce qu'une telle limite est triviale...
La règle de l'Hospital n'est enseignée ni au lycée ni en prépa en France (j'ignore ce qu'il en est des fac) : au lycée on ne voit pas de limites suffisamment compliquées pour faire appel à cette règle, et dans le supérieur on dispose des équivalents et dl. Je n'ai jamais eu à m'en servir donc j'aurais tendance à affirmer qu'on peut toujours s'en passer... Mais si vous avez un exemple de limite où les dl sont inefficaces ou vraiment lourds comparés à la règle de l'Hospital, je suis preneur.
La règle de l'Hospital n'est enseignée ni au lycée ni en prépa en France (j'ignore ce qu'il en est des fac) : au lycée on ne voit pas de limites suffisamment compliquées pour faire appel à cette règle, et dans le supérieur on dispose des équivalents et dl. Je n'ai jamais eu à m'en servir donc j'aurais tendance à affirmer qu'on peut toujours s'en passer... Mais si vous avez un exemple de limite où les dl sont inefficaces ou vraiment lourds comparés à la règle de l'Hospital, je suis preneur.
@miikou : merci pour le lien :zen:
nuage aussi se met à faire de l'humour :id:
oui... quand on connait les DL.
nuage a écrit:Sans la règle de L'Hospital comment calculer?
nuage aussi se met à faire de l'humour :id:
Imod a écrit:Cette règle est un artifice qui perd tout intérêt dès que l'on connait les développements limités alors pourquoi perdre son temps avec ?
Imod
oui... quand on connait les DL.
Skullkid a écrit:Comme Imod, je ne vois pas en quoiest un "bel exemple", c'est le genre de fonction qu'on utilise comme exemple pour introduire le prolongement par continuité, justement parce qu'une telle limite est triviale...
ok
Les limites du type
Skullkid a écrit: Mais si vous avez un exemple de limite où les dl sont inefficaces ou vraiment lourds comparés à la règle de l'Hospital, je suis preneur.
je préfère largement un calcul de DL à une suite de calculs de dérivées !
56 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
