bonjour a tous je bloque sur deux question d'un DM
soit la fonction f(x) = sin 2x - (racine de 3) cox2x
ecrie sous la forme Acos ( w x + phie )
et il me faut sa derivée
merci bcp
w= omega
Fonction dérivées
2 messages
- Page 1 sur 1
par Myers » 12 Déc 2005, 14:11
Salut
Pour mettre=\sin(2x)-\sqrt{3}\cos(2x))
sous la forme =A\cos(\omega x +\varphi))
tu développe )
avec la formule =\cos(a)\cos(b)-\sin(a)\sin(b))
.
Tu obtiens
=A\cos(\omega x)\cos(\varphi)-A\sin(\omega x)\sin(\varphi))
.
Puis tu identifie=g(x))
, tu obtient le système:
\cos(\varphi)=-\sqrt{3}\cos(2x) \\ <br />A\sin(\omega x)\sin(\varphi)=-\sin(2x)\end{array})
Il est évident que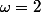
, tu simplifie , tu trouve
=-\sqrt{3} \\ <br />A\sin(\varphi)=-1\end{array})
Ensuite, tu cherche
tel que avec le cosinus tu obtient du 
et avec le sinus du 1. 
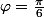convient tu as donc =\frac{\sqrt{3}}{2})
et =\frac{1}{2})
, tu remplace et il te rest juste a trouvez 
tel que
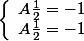
donc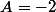
d'où=-2\cos\left(2x+\frac{\pi}{6}\right))
-----------------------------
Pour la dériver tu utilise la formule pour la composition)\big)}^\prime=g^\prime(x)f^\prime(g(x)))
Ici tu as=\cos(x))
et =2x+\frac{\pi}{6})
donc =-\sin(x))
et =2)
Ainsi
\right)}^\prime & = & -2 * 2 * -\sin\left(2x+\frac{\pi}{6}\right) \\ & = &4\sin\left(2x+\frac{\pi}{6}\right)\end{eqnarray})
Pour mettre
Tu obtiens
Puis tu identifie
Il est évident que
Ensuite, tu cherche
donc
d'où
-----------------------------
Pour la dériver tu utilise la formule pour la composition
Ici tu as
Ainsi
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :