Développement limité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
selma123
- Membre Relatif
- Messages: 189
- Enregistré le: 18 Sep 2008, 10:00
-
 par selma123 » 16 Oct 2008, 19:09
par selma123 » 16 Oct 2008, 19:09
salut
comment peux-je ecrire le developpement limité

à l'ordre 3 au point 0.
pouvez vous m'expliquer???
merci d'avance :hein:
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 16 Oct 2008, 19:24
par le_fabien » 16 Oct 2008, 19:24
Vu que

=
^{\frac{1}{2}})
Tu devrais t'aider de ça:
^a = 1+ax+\frac{a(a-1)}{2!}x^2+\frac{a(a-1)(a-2)}{3!}x^3+...+\frac{a(a-1)(a-2)...(a-n+1)}{n!}x^n+o(x^n))
-
selma123
- Membre Relatif
- Messages: 189
- Enregistré le: 18 Sep 2008, 10:00
-
 par selma123 » 16 Oct 2008, 23:25
par selma123 » 16 Oct 2008, 23:25
LEFAB11 a écrit:Vu que

=
^{\frac{1}{2}})
Tu devrais t'aider de ça:
^a = 1+ax+\frac{a(a-1)}{2!}x^2+\frac{a(a-1)(a-2)}{3!}x^3+...+\frac{a(a-1)(a-2)...(a-n+1)}{n!}x^n+o(x^n))
tu veux dire que
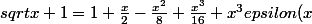)
-
Dr_Yahia
- Membre Naturel
- Messages: 14
- Enregistré le: 24 Mar 2008, 14:57
-
 par Dr_Yahia » 16 Oct 2008, 23:36
par Dr_Yahia » 16 Oct 2008, 23:36
kazoha19 a écrit:tu veux dire que
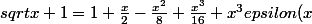)
Exactement c'est ca .
-
selma123
- Membre Relatif
- Messages: 189
- Enregistré le: 18 Sep 2008, 10:00
-
 par selma123 » 16 Oct 2008, 23:42
par selma123 » 16 Oct 2008, 23:42
Dr_Yahia a écrit:Exactement c'est ca .
a oui merci j'ai compris :id:
-
selma123
- Membre Relatif
- Messages: 189
- Enregistré le: 18 Sep 2008, 10:00
-
 par selma123 » 16 Oct 2008, 23:47
par selma123 » 16 Oct 2008, 23:47
alors pour log(x) que peux je faire????? :hein:
-
phryte
- Membre Irrationnel
- Messages: 1406
- Enregistré le: 05 Juil 2008, 17:09
-
 par phryte » 17 Oct 2008, 06:57
par phryte » 17 Oct 2008, 06:57
Slt.
Log(x) ? Mais on peut pour Log(1+x) !
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 17 Oct 2008, 08:54
par L.A. » 17 Oct 2008, 08:54
Bonjour.
le mieux dans le cas général pour trouver un développement limité reste le formule de Taylor-Young :
pour une fonction Cn+1 quand h -> 0
f(x+h) = somme(k=0 à n) [f^(k)(x)h^k/k!] + o(h^k)
-
selma123
- Membre Relatif
- Messages: 189
- Enregistré le: 18 Sep 2008, 10:00
-
 par selma123 » 17 Oct 2008, 10:15
par selma123 » 17 Oct 2008, 10:15
L.A. a écrit:Bonjour.
le mieux dans le cas général pour trouver un développement limité reste le formule de Taylor-Young :
pour une fonction Cn+1 quand h -> 0
f(x+h) = somme(k=0 à n) [f^(k)(x)h^k/k!] + o(h^k)
ok maerciiiiiiiiiiiiii :we: :id:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités