Etude de suite

[zelda007]

Salut,

On me demande d'étudier la suite u(n) = Somme(k=0..n) de 1/Sqrt(n² + k)

Alors pour le sens de variation, je fais u(n+1) - u(n) mais je suis bloqué déjà :(

Merci

[digardel]

pour un+1 - un c est pas trop dur;un+1=un + le terme de rang n+1 de ta somme

[zelda007]

Ah justement ej me posais la question, il faut pas aussi remplacer le n dans la somme par n+1 ?
Cad :

u(n+1) = Somme(k=0..n+1) de 1/Sqrt((n+1)²+k) ?

[zelda007]

Alors il faut remplacer tous les n par n+1 ou pas ?

[Doraki]

Oui, l'étude de l'éventuelle décroissance de la suite n'est pas aussi simple que ça.

C'est plus facile de montrer que la suite est convergente et de calculer sa limite.

[mathieuH]

tu es sur que ce n'est pas 1/Sqrt(n² + k²)?

[mathelot]

bjr,

si c'est du k, on peut utiliser le thm des gendarmes. Quel est le plus grand terme de cette somme de (n+1) termes ?

si c'est du k^2, c'est alors une somme de Riemann.

[Riemann mérite bien une majuscule. [AD])

[zelda007]

C'est bien "k" et de toute façon on a pas vu les sommes de Riemann.

Donc je pense que le plus grand terme est 1/sqrt(n² + 1) donc pour k = 1 non ?
Et comment faire avec le TDG pour calculer la limite ? et pour la monotonie ?

Merci

[mathelot]

La somme est constituée de (n+1) termes.

On connait le plus petit et le plus grand. comment encadre-t-on cette somme ?

[zelda007]

Y'a pas n termes dans la somme ? (k=1 à n)

Sinon, le plus grand c'est 1/sqtr(n²+1) (pour k = 1) et le plus petit c'est pour (k=n) donc 1/sqrt(n²+n)

non ?

Mais je ne vois pas comment conclure...

[yos]

Plus haut tu as mis de 0 à n, donc n+1 termes.
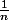
Le plus grand est donc . D'où .
De même tu minores .
Finalement on trouve que converge vers 1.
On peut faire un encadrement plus fin utilisant .
Mais ces encadrements ne donnent pas la monotonie de
Tu es sûr qu'on en a besoin?

[zelda007]

non en fait on avait pas besoin de la monotonie !

Merci :)