Exo suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Oct 2008, 18:21
par leon1789 » 11 Oct 2008, 18:21
flo10 a écrit:Un = U1 * q^n-1 ?
nan,
la somme ! :ptdr: u0 + u1 + ... + un = ....
-
flo10
- Membre Relatif
- Messages: 136
- Enregistré le: 06 Nov 2007, 18:51
-
 par flo10 » 11 Oct 2008, 19:06
par flo10 » 11 Oct 2008, 19:06
non ... pas vu. C'est quoi la formule?
-
niki112
- Membre Naturel
- Messages: 28
- Enregistré le: 28 Oct 2007, 17:04
-
 par niki112 » 11 Oct 2008, 19:24
par niki112 » 11 Oct 2008, 19:24
J'ai le meme exo a faire et je bloque aussi pour la 3 et la 4!! :cry:
need help please

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Oct 2008, 19:25
par leon1789 » 11 Oct 2008, 19:25
flo10 a écrit:non ... pas vu. C'est quoi la formule?
tu es certain(e) de toi ? on te demande de calculer la somme des termes d'une suite géométrique, mais le prof ne t'a pas donné la formule dans le cours ?
-
flo10
- Membre Relatif
- Messages: 136
- Enregistré le: 06 Nov 2007, 18:51
-
 par flo10 » 11 Oct 2008, 19:43
par flo10 » 11 Oct 2008, 19:43
Non je n'ai pas vu, ça....c'est pour ça que je bloque vraiment a la3) et 4).

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Oct 2008, 19:49
par leon1789 » 11 Oct 2008, 19:49
ok, alors changement d'épaule !
flo10 a écrit:3)Démontrer que : n appartient à N, 1+1/2 +1 /2² +1/2^3 +.....+ 1/2n-1 = 2* (1-(1/2)^n).
Par récurrence sur

, c'est assez facile, non ?
-
niki112
- Membre Naturel
- Messages: 28
- Enregistré le: 28 Oct 2007, 17:04
-
 par niki112 » 11 Oct 2008, 19:56
par niki112 » 11 Oct 2008, 19:56
il faut démontrer la 3 par recurrence?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Oct 2008, 19:58
par leon1789 » 11 Oct 2008, 19:58
niki112 a écrit:il faut démontrer la 3 par recurrence?
si vous n'avez pas de formule dans le cours que l'on puisse utiliser d'un coup,
alors une petit récurrence est nécessaire.
-
niki112
- Membre Naturel
- Messages: 28
- Enregistré le: 28 Oct 2007, 17:04
-
 par niki112 » 11 Oct 2008, 20:04
par niki112 » 11 Oct 2008, 20:04
c'est quoi la formule dont vous palez?
-
flo10
- Membre Relatif
- Messages: 136
- Enregistré le: 06 Nov 2007, 18:51
-
 par flo10 » 11 Oct 2008, 20:08
par flo10 » 11 Oct 2008, 20:08
on sait que Un = U0 qn
et Un = 1 +1/1! +1/2! + ...+ 1/n!
Mais je ne sais pas comment faire pour démontrer la question3) avec ça.
-
niki112
- Membre Naturel
- Messages: 28
- Enregistré le: 28 Oct 2007, 17:04
-
 par niki112 » 11 Oct 2008, 20:14
par niki112 » 11 Oct 2008, 20:14
vous parliez de la formule de la somme des termes consecutifs d'une suite géométrique non?
J'ai ca:
U0* (1-q^n)/(1-q) ou q est la raison et U0 le premier terme

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Oct 2008, 20:18
par leon1789 » 11 Oct 2008, 20:18
flo10 a écrit:on sait que Un = U0 qn
et Un = 1 +1/1! +1/2! + ...+ 1/n!
Mais je ne sais pas comment faire pour démontrer la question3) avec ça.
Mais vous cherchez des trucs compliqués avec les factorielles !!! Il n'y a besoin de rien pour faire une récurrence prouvant
pour tout n appartient à N,
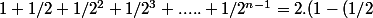^n))
.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Oct 2008, 20:19
par leon1789 » 11 Oct 2008, 20:19
niki112 a écrit:vous parliez de la formule de la somme des termes consecutifs d'une suite géométrique non?
J'ai ca:
U0* (1-q^n)/(1-q) ou q est la raison et U0 le premier terme
oui exactement.
-
flo10
- Membre Relatif
- Messages: 136
- Enregistré le: 06 Nov 2007, 18:51
-
 par flo10 » 11 Oct 2008, 20:28
par flo10 » 11 Oct 2008, 20:28
oui mais comment on fait aprés?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Oct 2008, 20:29
par leon1789 » 11 Oct 2008, 20:29
flo10 a écrit:oui mais comment on fait après?
après quoi ?
-
flo10
- Membre Relatif
- Messages: 136
- Enregistré le: 06 Nov 2007, 18:51
-
 par flo10 » 11 Oct 2008, 20:45
par flo10 » 11 Oct 2008, 20:45
leon1789 a écrit:oui exactement.
quand on a ça?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Oct 2008, 20:50
par leon1789 » 11 Oct 2008, 20:50
flo10 a écrit:quand on a ça?
quand on a quoi ? la récurrence à faire ou la formule à appliquer ?
-
flo10
- Membre Relatif
- Messages: 136
- Enregistré le: 06 Nov 2007, 18:51
-
 par flo10 » 11 Oct 2008, 20:54
par flo10 » 11 Oct 2008, 20:54
beh la récurrence à faire pour démontrer la formule?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 11 Oct 2008, 20:56
par leon1789 » 11 Oct 2008, 20:56
flo10 a écrit:beh la récurrence à faire pour démontrer la formule?
tu as fait la récurrence ?
-
flo10
- Membre Relatif
- Messages: 136
- Enregistré le: 06 Nov 2007, 18:51
-
 par flo10 » 11 Oct 2008, 21:07
par flo10 » 11 Oct 2008, 21:07
non je sais pas comment faire
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités