Limite de de f(a_n)
14 messages
- Page 1 sur 1
Limite de de f(a_n)
Bonjour !
Jai un problème qui doit sûrement être simple à résoudre, mais je ne sais pas par où partir
E et F métriques avec F complet. A une partie de E.
Soit f de A dans F uniformément continue.
Soit (a_n) une suite de A qui converge vers x dans E
On sait : f(a_n) converge vers b dans F
Comment montrer que b ne dépend que de x et pas de (a_n).
Lexercice en lui-même est plus long donc je pense quil y a des données qui ne doivent pas servir mais je ne vois franchement pas comment montrer cela par labsurde peut être
Merci davance !
Jai un problème qui doit sûrement être simple à résoudre, mais je ne sais pas par où partir
E et F métriques avec F complet. A une partie de E.
Soit f de A dans F uniformément continue.
Soit (a_n) une suite de A qui converge vers x dans E
On sait : f(a_n) converge vers b dans F
Comment montrer que b ne dépend que de x et pas de (a_n).
Lexercice en lui-même est plus long donc je pense quil y a des données qui ne doivent pas servir mais je ne vois franchement pas comment montrer cela par labsurde peut être
Merci davance !
leon1789 a écrit:Je ne pense pas, car x est fixé, donc la continuité suffit.
(En plus, il n'y a pas d'hypothèse pour justifier l'uniforme continuité.)
Après rectification de l'énoncé due à la remarque de Yos, f n'est pas uniformément continue sur E mais seulement sur A et x n'est pas forcément dans A
bonsoir,
soient deux suites a et u qui converge vers x.
on les mixe en définissant la suite c:
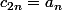

c est une suite convergente donc de Cauchy.
soit
on choisit grâce à l'uniforme continuité tel que
grâce à l'uniforme continuité tel que
si < \alpha) alors
alors ,f(x')) < \epsilon)
on en déduit que) est une suite de Cauchy.
est une suite de Cauchy.
or, une de ses suites extraites) converge vers b.
converge vers b.
d'où=f(u_n)) converge aussi vers b.
converge aussi vers b.
Ceci montre qu'une fonction uniformément continue dans un voisinage
épointé de se prolonge en
se prolonge en 
soient deux suites a et u qui converge vers x.
on les mixe en définissant la suite c:
c est une suite convergente donc de Cauchy.
soit
on choisit
si
on en déduit que
or, une de ses suites extraites
d'où
Ceci montre qu'une fonction uniformément continue dans un voisinage
épointé de
mathelot a écrit:bonsoir,
soient deux suites a et u qui converge vers x.
on les mixe en définissant la suite c:
c est une suite convergente donc de Cauchy.
soit
on choisitgrâce à l'uniforme continuité tel que
sialors
on en déduit queest une suite de Cauchy.
or, une de ses suites extraitesconverge vers b.
d'oùconverge aussi vers b.
Ceci montre qu'une fonction uniformément continue dans un voisinage
épointé dese prolonge en
Bj
Ca me parait un peu compliqué. Est-ce qu'on ne peut pas dire plus simplement:
d(an,un) tend vers zéro
Doù (uniforme continuité) d(f(an),f(un)) tend vers zéro
Puis d(f(bn),b) <= d(f(bn),f(an)) + d(f(an),b)
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
