Série de fourier
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
par ptitmatteo » 08 Oct 2008, 20:37
= \frac{\pi ^2}{3} - 4 cos (w) + cos( 2.w) - \frac{4}{9} cos (3.w) .........)
= \frac{\pi ^2}{3} - 4 + 1 - \frac{4}{9} .........)
lorsque t=0
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
par Joker62 » 08 Oct 2008, 20:51
J'imagine qu'un coup de Parseval arrange tout ça :)
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
par ptitmatteo » 08 Oct 2008, 20:56
le problème c'est qu'en cours on la pas appris
-
mathelot
par mathelot » 08 Oct 2008, 21:01
bonsoir,
=\sum_{n \geq 1} \, n^{-2})
en séparant les indices pairs et impairs
=\sum_{n \geq 0 } \, {(2n+1)}^{-2})
en faisant t=0
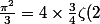 - \zeta(2))
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
par ptitmatteo » 08 Oct 2008, 21:12
j'ai pas tout saisi
-
mathelot
par mathelot » 08 Oct 2008, 21:25
ptitmatteo a écrit:j'ai pas tout saisi
faire t=0.
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
par ptitmatteo » 08 Oct 2008, 21:30
lorsque t=0
-
mathelot
par mathelot » 08 Oct 2008, 21:42
ptitmatteo a écrit:lorsque t=0
non, il faut aussi remplacer à gauche t par 0.
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
par ptitmatteo » 09 Oct 2008, 07:39
= \frac{\pi ^2}{3} - 4 cos (w) + cos( 2.w) - \frac{4}{9} cos (3.w) .........)
= \frac{\pi ^2}{3} - 4 + 1 - \frac{4}{9} .........)
lorsque t=0
et c'est tout?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
