Etude fonction

[mari2]

Bonjours je voudrai avoir une petite aide pour cette exercice.

On considère les fonctions f et g définies sur R par:

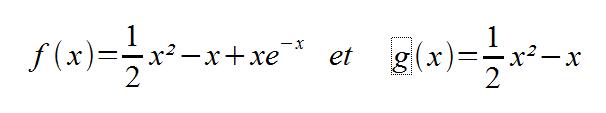
On notera Cf et Cg les courbes représentatives de ces fonctions dans un repère orthonormal (unité graphique: 2cm).
1.Montrer que f(x) peut s'écrire sous la forme:

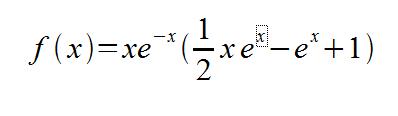
En déduire la limite de f en -oo.
2.a)Déterminer la limite de f en +oo.
b)On considère la fonction h définie sur R par h(x)=f(x)-g(x).
Déterminer la limite de h en +oo.
Donner une interprétation graphique de ce résultat.
c)En utilisant le signe de h(x), étudier la position relative des courbes Cf et Cg.

Merci d'avance.

[Plastoc]

Tu a un problème où dans l'exo? ^^

[mari2]

pour la 1er question je ne vois pas comment on peut retrouver f(x) pcq les e^(x) me gene un peu

[Plastoc]

C'quoi le logiciel que tu utilise pour écrire comme ça? ^^

Juste pour que tu comprenne mieux parce que écrire comme ça c'est un peu l'embrouille ^^.

[mari2]

open source math lol

[Plastoc]

Bon en fait on vas partir de ce que tu dois trouvé pour avoir ce que tu a au début.

Donc on a f(x)=xe^-x(1/2xe^x-e^x+1)

Tu sais que e^x marche comme les puissances donc on vas développer petit a petit.

Tout d'abord:

xe^-x*1/2xe^x=x*x*1/2*e^-x*e^x (J'ai juste rassembler les x,et e^x entre eux pour tu comprenne.

donc ça donne x²*1/2*e^(-x+x) (Car e^a + e^b = e^(a+b) ici a=-1 et b=1)

=(1/2)x²*e^0 car e^(-x+x)=e^0 et e^0=1

alors = (1/2)x²

Ensuite:

xe^-x*(-e^x)= -x*e^-x*e^x
= -x*e^(-x+x) donc e^0=1
= -x

Enfin:

ex^-x*1=ex^-x

donc tu a bien au final (1/2)x²-x+xe^-x

[mari2]

Je trouve ça c'est bon ?

[Plastoc]

Oui suffit juste de partir de ce que tu dois trouver pour arriver a ce que tu a ^^. Si c'est le cas c'est bon. Et pour les expo c'est pareil que les puissances ^^ donc c'pas si dur a utiliser :p.

[mari2]

Ok est pour la suite je doit faire quoi ?

[Plastoc]

En déduire la limite de f en -oo.

Etudie la lim quand x tend vers -oo de f(x).

[mari2]

Mais la c une forme indéterminé comment je fais ?

[mari2]

Qui peut m'aider pour la suite s'il vous plait Merci