Fonction continue
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
takusan
- Membre Naturel
- Messages: 14
- Enregistré le: 04 Oct 2008, 14:38
-
 par takusan » 04 Oct 2008, 14:39
par takusan » 04 Oct 2008, 14:39
Bonjour notre professeur nous a donné un dm dont je ne comprend aboslument rien:
Il faut trouver :
Une fonction continue en aucun point
Une fnction continue mais dérivable en aucun point
Une fonction non constance sur R dont la dérivée est indentiquement nulle sur un intervalle ouvert
Une fonction stricetement croissante et pas dérivable (f(x)=x avec x < o et f(x)=0.5x avec x>0
merci d'avance c'est assez urgent
 par Dominique Lefebvre » 04 Oct 2008, 15:19
par Dominique Lefebvre » 04 Oct 2008, 15:19
takusan a écrit:Bonjour notre professeur nous a donné un dm dont je ne comprend aboslument rien:
Il faut trouver :
Une fonction continue en aucun point
Une fnction continue mais dérivable en aucun point
Une fonction non constance sur R dont la dérivée est indentiquement nulle sur un intervalle ouvert
Une fonction stricetement croissante et pas dérivable (f(x)=x avec x 0
merci d'avance c'est assez urgent
Bonjour,
Bien sur, tu connais les définitions d'une fonction continue et dérivable .... parce qui si oui, qu'attends tu de nous? Sinon, il est temps de les apprendre... C'est urgent même !
-
takusan
- Membre Naturel
- Messages: 14
- Enregistré le: 04 Oct 2008, 14:38
-
 par takusan » 04 Oct 2008, 15:21
par takusan » 04 Oct 2008, 15:21
oui je connais les definitions mais le professeur nous demande de donner des expression de ces fonction et je n'arrive pas a en trouver
 par Dominique Lefebvre » 04 Oct 2008, 15:24
par Dominique Lefebvre » 04 Oct 2008, 15:24
takusan a écrit:oui je connais les definitions mais le professeur nous demande de donner des expression de ces fonction et je n'arrive pas a en trouver
Un peu d'imagination ! Quelle tête pourrait avoir une fonction discontinue en tous points.Prend la définition de la continuité et renverse là. Que deviendrait la définition d'une fonction discontinue en tous points ?
-
takusan
- Membre Naturel
- Messages: 14
- Enregistré le: 04 Oct 2008, 14:38
-
 par takusan » 04 Oct 2008, 15:28
par takusan » 04 Oct 2008, 15:28
Une fonction continue c'est bien quand limf(x)=f(a) quand x tend vers a ?
Je n'arrive pas a trouver les expression avec cette definiton
La fonction partie entiere n'est pas discontinue en tout point ?
 par Dominique Lefebvre » 04 Oct 2008, 15:46
par Dominique Lefebvre » 04 Oct 2008, 15:46
takusan a écrit:Une fonction continue c'est bien quand limf(x)=f(a) quand x tend vers a ?
Je n'arrive pas a trouver les expression avec cette definiton
La fonction partie entiere n'est pas discontinue en tout point ?
Pose toi la question de savoir s'il y a un point de cette fonction tel que ce point réponde à la définition de la continuité...
-
takusan
- Membre Naturel
- Messages: 14
- Enregistré le: 04 Oct 2008, 14:38
-
 par takusan » 04 Oct 2008, 15:49
par takusan » 04 Oct 2008, 15:49
Fonction continue en aucun point: La fonction partie entière?
Fonction continue et derivable en aucun point : f(x) = valeur absolue de x quand x=0?
Fonction non constante dont la derivée est identiquement nulle sur un intervalle ouvert f(x)=x quand x=0
ralalala je comprend rien :mur:
-
takusan
- Membre Naturel
- Messages: 14
- Enregistré le: 04 Oct 2008, 14:38
-
 par takusan » 04 Oct 2008, 15:53
par takusan » 04 Oct 2008, 15:53
Dominique Lefebvre a écrit:Un peu d'imagination ! Quelle tête pourrait avoir une fonction discontinue en tous points.Prend la définition de la continuité et renverse là. Que deviendrait la définition d'une fonction discontinue en tous points ?
Ca serait un nuage de point ? quelle expression pourrait-elle avoir ? :triste:
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 04 Oct 2008, 16:01
par Zweig » 04 Oct 2008, 16:01
Une fonction continue en aucun point
Par exemple la fonction
 = 1)
si
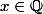
, 0 sinon.
-
takusan
- Membre Naturel
- Messages: 14
- Enregistré le: 04 Oct 2008, 14:38
-
 par takusan » 04 Oct 2008, 16:03
par takusan » 04 Oct 2008, 16:03
mon prof m'avais dit que f(x)=1 était une equation et non une fonction
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 04 Oct 2008, 16:05
par Zweig » 04 Oct 2008, 16:05
Private joke ?
-
takusan
- Membre Naturel
- Messages: 14
- Enregistré le: 04 Oct 2008, 14:38
-
 par takusan » 04 Oct 2008, 16:12
par takusan » 04 Oct 2008, 16:12
takusan a écrit:Une fonction continue mais dérivable en aucun point
f(x)=x quand x appartient aux entier ?
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 04 Oct 2008, 16:15
par Monsieur23 » 04 Oct 2008, 16:15
Une fnction continue mais dérivable en aucun point
Euh... C'est hard comme question ça, pour le lycée, non ?
« Je ne suis pas un numéro, je suis un homme libre ! »
-
takusan
- Membre Naturel
- Messages: 14
- Enregistré le: 04 Oct 2008, 14:38
-
 par takusan » 04 Oct 2008, 16:17
par takusan » 04 Oct 2008, 16:17
déjà que je suis pas bon en math mon prof si c'est pas de notre niveau j'ai plus qu'a trouver une corde
Mais est-ce que vous sauriez repondre au autres parce que j'ai cherché de partout je trouve rien
-
takusan
- Membre Naturel
- Messages: 14
- Enregistré le: 04 Oct 2008, 14:38
-
 par takusan » 04 Oct 2008, 16:47
par takusan » 04 Oct 2008, 16:47
Personne pourrait m'aider avec un gros coup de pouce....
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 04 Oct 2008, 16:48
par Monsieur23 » 04 Oct 2008, 16:48
La fonction de Zweig marche bien hein.
« Je ne suis pas un numéro, je suis un homme libre ! »
-
takusan
- Membre Naturel
- Messages: 14
- Enregistré le: 04 Oct 2008, 14:38
-
 par takusan » 04 Oct 2008, 16:50
par takusan » 04 Oct 2008, 16:50
euh fonction de quoi ? vous pensez que ca passerai si je met une fonction que j'ai jamais vu de ma vie?
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 04 Oct 2008, 16:53
par Monsieur23 » 04 Oct 2008, 16:53
Zweig a écrit:Par exemple la fonction
 = 1)
si
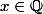
, 0 sinon.
C'est de cette fonction là que je parle ! :ptdr:
« Je ne suis pas un numéro, je suis un homme libre ! »
-
takusan
- Membre Naturel
- Messages: 14
- Enregistré le: 04 Oct 2008, 14:38
-
 par takusan » 04 Oct 2008, 16:57
par takusan » 04 Oct 2008, 16:57
aaa ok lol et sinon pour les autres question tu pourrai me donner des expression parce que j'ai cherché de partout sur internet ainsi que mon livre de math et je trouve rien du tout
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 04 Oct 2008, 17:04
par Zweig » 04 Oct 2008, 17:04
C'est dans ta tête qu'il faut chercher ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 99 invités
