Action de groupe

[digardel]

bonjour
Le goupe affine du plan, le groupe des isométries et des similitudes agissent de façon triviale sur l'ensemble C des coniques.
Je voudrais trouver l'orbite de chaque élément de C.

Pour le groupe affine ce n'est pas trop dur, du moins si je ne me suis pas trompé dans mon raisonnement.
Si E est une ellipse d'équation x²+y²=1 dans un repère (O;i;j) et T une transformation affine alors T(E) est l'ellipse d'équation x²+y²=1 dans le repère (T(O);T'(i); T'(j)) où T' est l'ap linéaire associée. Une petite réciproque et on montre que l'orbite d une ellipse est l'ensemble des ellipses, de même pour une parabole et une hyperbole.

En procédant de la même façon je suis arrivé à prouver que pour l'action du groupe des similitudes l'orbite d'une ellipse est l'ensemble des ellipses de même demi-axes, celle d'une parabole, les paraboles associées au même paramètres

Mon problème, c'est pour l'action du groupe des similitudes, je ne vois pas comment m'y prendre...
Merci

[yos]

Tu crois vraiment que c'est pour le groupe affine que c'est le plus simple?
Sinon : une similitude conserve l'excentricité et inversement, deux coniques de même excentricité sont semblables.

[COTLOD]

Quelles caractérisations de chaque type conique peux-tu utiliser?

[digardel]

Ok , je pense que j ai fini.Merci de votre aide.
Ps çà me parait simple pour lr groupe affine car une conique est transformée en une conique de meme equation dans un autre repère.....mais peut-être que je fais une erreur de raisonnement,ce serait pas la première...

[yos]

je suis arrivé à prouver que pour l'action du groupe des similitudes l'orbite d'une ellipse est l'ensemble des ellipses de même demi-axes, celle d'une parabole, les paraboles associées au même paramètres

Tu voulais dire "isométries"?

Mon problème, c'est pour l'action du groupe des similitudes, je ne vois pas comment m'y prendre...

Tu as dû trouver que l'orbite d'une conique C est l'ensemble des coniques de même excentricité que C.

[digardel]

oui c est çà er je cherche maintenant les stabilisateurs.Pour les ellipses c est pas trop dur en passant par un cercle dont l ellipse est dans l orbite,pour le reste je décolle pas

[yos]

Là encore, c'est facile pour les similitudes et les isométries (d'ailleurs les stabilisateurs d'une conique C coïncident dans ces deux cas sauf si C est une conique dégénérée comme un point ou une droite).
Pour le groupe affine, c'est un peu plus dur : si une bijection affine conserve une ellipse E, elle fixe son centre, et permute ses sommets (à vérifier). Par ailleurs une bijection affine est déterminée par l'image de trois points non alignés donc on peut s'en sortir. Je pense que si E n'est pas un cercle,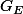 contient les isométries obtenues plus haut ainsi que quelques affinités orthogonales.

[digardel]

Bonjour,pour le groupe affine j y suis arrivé pour les ellipses.En fait ,l idée est de se ramener a un cercle .En effet,si E est une ellipse,elle est dans l orbite d 'un cercle C et trouver les stabilisateur d 'un cercle c est pas trop dur,même si je m en suis vu pour etre rigoureux.
Apres on conclut, que si M est dans le stabilisateur du cercle et que T est telle que T(C)=M alors le stabilisateur de E est l ensemble des T^-1 M T

on trouve donc S (E)= l ensemble des T^-1 M T avec M dans le groupe orthogonal et T est l automorphisme qui laisse stable le centre de l ellipse et de matrice.
a 0
0 b

Le stabilisateur pour le cercle n'est autre que le groupe orthogonal (de la forme quadratique x2+y2). Pour l'hyperbole, ça me donne pas une petite idée de ce que ça pourrait être .Je creuse.

[yos]

Apres on conclut, que si M est dans le stabilisateur du cercle et que T est telle que T(C)=M alors le stabilisateur de E est l ensemble des T^-1 M T

T(C)= E je suppose??
Auquel cas et pas il me semble.

Le stabilisateur pour le cercle n'est autre que le groupe orthogonal (de la forme quadratique x2+y2). Pour l'hyperbole, ça me donne pas une petite idée de ce que ça pourrait être .Je creuse.

Je préfère un raisonnement plus géométrique mais c'est toi qui voit.
Une hyperbole H est dans l'orbite de l'hyperbole équilatère x^2-y^2=1 dont le groupe doit pas être plus dur à déterminer que pour le cercle

[Maxmau]

Bj
je prends le train en marche

Ok pour le stabilisateur du cercle dans le cas du groupe affine
(ca se fait très bien analytiquement)

Tu peux essayer analytiquement avec l'hyperbole équilatère comme le suggère Yos. Interviennent sans doute les lignes hyperboliques en place des lignes trigonométriques

méthode analogue pour la parabole ?

[digardel]

T as raison yos, c est TGcT^-1 faute de frappe