Petit problème de maths :
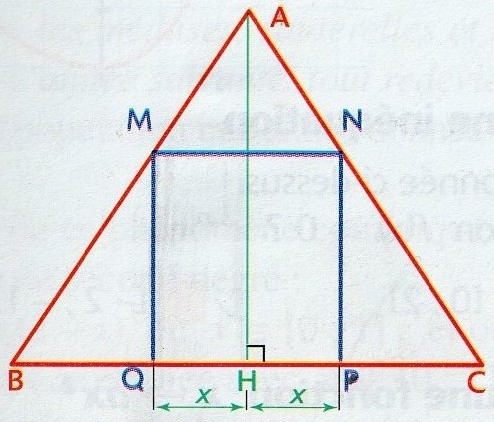
ABC est un triangle isocèle en A avec BC=12
H est ke pied de la hauteur issue de A et AH=9
P et Q sont deux points de [BC] symétriques par rapport à H, on note HP=HQ=x
On se propose de déterminer les dimensions du rectangle MNPQ d'aire maximale inscrit dans ce triangle.
1)a. Démontrer que MQ=18-3x/2
Sur cette première question je me demande dans quel triangle nous devons travailler (BMQ ? BMC ?), est-il necéssaire de connaître AB et AC ? ( Qui sont facile à trouver =) )
Merci de votre aide
