Trace
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
may prepa
- Membre Naturel
- Messages: 30
- Enregistré le: 12 Avr 2008, 16:31
-
 par may prepa » 21 Sep 2008, 15:13
par may prepa » 21 Sep 2008, 15:13
bonjour,
je réfléchis depuis un petit moment sur un exercice :
montrer que (pour tout X appartenant Mn(K)) avec A,B appartenant à (Mn(K))^2 :
tr(AX)=tr(BX) => A=B
j'ai essayé d'écrire AX et BX sous la forme d'une somme:
AX=somme(a(ij)x(ij).E(ij)) mais ça ne m'aide pas pour prouver l'implication pourriez vous m'aidez s'il vous plait.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Sep 2008, 15:17
par yos » 21 Sep 2008, 15:17
Prends
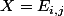
.
-
may prepa
- Membre Naturel
- Messages: 30
- Enregistré le: 12 Avr 2008, 16:31
-
 par may prepa » 21 Sep 2008, 15:25
par may prepa » 21 Sep 2008, 15:25
je ne comprend pas, si je prend X=E(ij), je crois que j'ai tr(AX)=tr(A) et tr(BX)=tr(B),mais je ne vois pas en quoi cela prouve que A=B.
je veut dire que par exemple la somme des termes diagonaux peut être la même pour deux matrices sans que ces termes soient égaux.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 21 Sep 2008, 15:57
par Joker62 » 21 Sep 2008, 15:57
Pour une matrice A quelconque :
On a Tr(A.Eij) = (A)ji
-
may prepa
- Membre Naturel
- Messages: 30
- Enregistré le: 12 Avr 2008, 16:31
-
 par may prepa » 21 Sep 2008, 16:02
par may prepa » 21 Sep 2008, 16:02
et j'ai le droit de prendre une matrice X=E(ij) parce que dans ce cas je ne traite que un cas quelconque non?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 21 Sep 2008, 16:22
par Joker62 » 21 Sep 2008, 16:22
C'est vrai pour toutes les matrices, donc en particulier pour les matrices élémentaires.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 21 Sep 2008, 16:25
par Joker62 » 21 Sep 2008, 16:25
Désolé j'ai répondu à côté...
Les matrices élémentaires forment une base de l'espace des matrices.
Il suffit donc de le prouver pour ces matrices en particulier.
Désolé encore.
-
may prepa
- Membre Naturel
- Messages: 30
- Enregistré le: 12 Avr 2008, 16:31
-
 par may prepa » 21 Sep 2008, 17:10
par may prepa » 21 Sep 2008, 17:10
d'accord :) merci beaucoup pour l'aide j'ai compris maintenant!!
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 21 Sep 2008, 17:25
par yos » 21 Sep 2008, 17:25
Joker62 a écrit:Désolé j'ai répondu à côté...
Les matrices élémentaires forment une base de l'espace des matrices.
Il suffit donc de le prouver pour ces matrices en particulier.
Désolé encore.
Ben non : c'est ta précédente réponse qui est correcte. Peu importe que les Eij forment une base ici.
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 22 Sep 2008, 13:17
par Joker62 » 22 Sep 2008, 13:17
En effet ! Me suis embrouillé tout seul :^)
Désolé.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
