-1 = 2

[leon1789]

Suite à un sujet d'Acoustica, je propose une preuve (évidemment fausse mais amusante je trouve) de -1 = 2.

Soit f la fonction .

On a : on dit que -1 est un point fixe de f.

Du coup, par une récurrence évidente, pour tout ,
on a

Autrement dit (*) (avec n traits de fractions).

Par ailleurs, on vérifie (cf développement en fractions continues) que
(avec une infinité de traits de fractions).

Du coup, on reprend l'égalité (*) et on passe aux limites (elles existent !) en faisant tendre n vers l'infini : il vient alors

Non ? :hein:

[miikou]

bah evidement que non, ces deux devellopement en fraction non rien a voir ..

[leon1789]

bah evidement que non, ces deux devellopement en fraction non rien a voir ..

pourquoi ?

[informix]

je suis curieux de connaitre pourquoi le NON lool ? sachant qu'il doit y avoir une explication à cette contradiction...

[Euler911]

Quelle absurdité! :ptdr:

[informix]

[cite]développement en fractions continues[/cite]

pouvez-vous svp rappeler le principe des Dev en Fractions continues? :hum:

[Doraki]

2 et -1 sont les deux points fixes de la fonction utilisée.
Sauf que 2 est attracteur et pas -1.

[leon1789]

Quelle absurdité! :ptdr:

Il en faut, il en faut ! :ptdr:
En fait, tout est correct sauf un "petit" truc (qui n'est pas visible dans l'énoncé). L'explication de la contradiction est très compréhensible quand ce "petit" truc est explicité.

2 et -1 sont les deux points fixes de la fonction utilisée.
Sauf que 2 est attracteur et pas -1.

ahhhhhhh, c'est ça, mais pourquoi 2 est-il l'attracteur (kesako ?) et non -1 ?


Edit : Si tu ne donnes pas la réponse, je le ferai :we:

[leon1789]

pouvez-vous svp rappeler le principe des Dev en Fractions continues? :hum:

oula. Sur wikipédia, il doit y a une introduction à cela.

[Doraki]

La différence entre tes deux écritures infinies est que y'en a une où tu sais par quoi ça se termine (1+2/-1), et que l'autre tu dis rien sur comment interpréter la fin de ton écriture (2/(1+...))

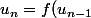Généralement le comportement de la suite dépend du premier terme de la suite.
Ici, 2 et -1 sont deux limites possibles de la suite.

f'(x) = -2/x².
|f'(2)| = |-2/4| = 1/2 1. Ca implique que même si x est proche de -1, f(x) s'éloignera de -1.
Il ne peut pas y avoir de suite qui tend vers -1 à moins que la suite soit stationnaire,
et ça dit que l'ensemble des valeurs initiales qui vont générer une suite qui tend vers -1 est fermé (et dénombrable dans notre cas)

Ici, on peut dire que l'ensemble des valeurs initiales qui générent une suite qui tend vers 2 est un ouvert dense de R, et que si on devait donner un sens à l'écriture infinie f(f(f(...))), ben c'est la limite 2 qu'on devrait prendre.

[leon1789]

Merci :zen: Oui, c'est une explication quand on définit une suite par itération de fonction.

Voici mon explication, revenant à la définition des fractions continues, mais assez calculatoire.

En partant d'un réel , on considère la suite pour n>0 :

Evidemment, pour ,on évitera les valeurs critiques (au plus dénombrables) annulant un dénominateur : 0, , , etc.

Via un peu d'algèbre linéaire, on montre que
(Remarquer que, dans cette écriture, apparaissent bien les points fixes de f, qui sont -1 et 2)

Alors la suite possède une limite qui est 2 (car |2|>|-1|) ...sauf si ! Et si alors pour tout n.

[Euler911]

A quel niveau d'étude est-on sencé comprendre tout ça???

ça veut dire quoi "au plus dénombrables"???

***EDIT: lire censé au lieu de "sencé" ***

[leon1789]

ça veut dire quoi "au plus dénombrables"???

Un ensemble au plus dénombrable est soit de cardinal fini, soit en bijection avec l'ensemble des entiers naturels.

A quel niveau d'étude est-on sensé comprendre tout ça???

Là, sur ce que j'ai écrit, il y a :

-- le coup des entiers à éviter, sinon la suite n'est pas définie. Comprendre qu'il existe finalement "peu" d'éléments pathologiques dans R, c'est du niveau L1 je pense.

-- des histoires de suites, de limites, de croissances comparées des monômes en fonction de d (je dirais niveau TS).

-- pour la formule , il y a deux niveaux d'approche : soit on le prouve par récurrence (niveau TS), soit on redécouvre le résultat par un peu d'algèbre linéaire (je dirais niveau L1-L2).

[Euler911]

Un ensemble au plus dénombrable soit de cardinal fini, soit en bijection avec l'ensemble des entiers naturels.

Ben Didon, c'est compliqué tout ça! (je vais aller rendre visite à mon ami Wiki je pense...)

-- le coup des entiers à éviter, sinon la suite n'est pas définie. [...]
-- pour la formule , il y a deux niveaux d'approche : [...]

En gros, c'est pas encore de mon niveau: je passe!:D