Ensembles et applications

[boostbasket]

Bonjour a tous, j'ai un exercice au sujet d'applications et d'ensembles qui me pose probleme, j'espère que vous pourrez m'aider.
Soit E un ensemble, (A,B) E P(E)²
Soit f: P(E) --->P(A) x P(B)
X --->(A inter x,B inter x)

1) Montrer que f est injective AUB = E
2) Montrer que f est surjective A inter B = Ensemble vide
( Indications : pour une implication, on regardera l'ensemble d'arrivée (A, Ensemble vide) et pour l'autre on cherchera M E P(E) tel que (M inter A,M inter B)=(x,y) avec (x,y) E P(A) x P(B))
3) En déduire une Condition Nécessaire et Suffisante pour que f soit bijective. (On dira que A et B forment une partition de E)

Merci d'avance

[busard_des_roseaux]

bonjour,


si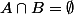

soit (U,V) quelconque dans P(A)xP(B)
d'où

on pose



donc f est surjective

si f est surjective,
est la trace sur A
d'une partie X de E qui ne rencontre pas B.
d'où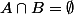



----------------------------

Si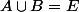

une partie X quelconque de E s'écrit


d'où si f(X)=(L,M) , et

posons

de manière évidente


f est inversible à gauche donc injective.


------------------------

si f est injective,