Produit vectoriel

[HH.What?]

Soit un repère orthonormé , trouver les deux vecteurs et tels que :


;)

(Comment faire le signe produit vectoriel svp?)

Mon problème est que je ne sais pas par ou commencer en fait.
Je viens à peine de découvrir le produit vectoriel, je ne sais pas comment l'utiliser :S

[XENSECP]

ba tu peux voir ça géométriquement par exemple ;) Mais je pense que la méthode bourrin marche aussi (poser 6 inconnues et avoir 6 équations)

[HH.What?]

Désolé, mais je ne saisis pas comment faire :S

[mathelot]

Mon problème est que je ne sais pas par ou commencer en fait.
Je viens à peine de découvrir le produit vectoriel, je ne sais pas comment l'utiliser :S

bjr,

On suppose un espace vectoriel E de dimension 3 orienté.

1)
le produit vectoriel est un produit.
Il est donc linéaire par rapport au 1er vecteur et par rapport au second.
on peut donc utiliser la double distributivité.

Il est antisymétrique. Quand on permute les deux vecteurs,
le produit est changé en son opposé.

Il est donc alterné,ie,

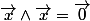
2)
Quand on développe les deux vecteurs et dans une base i,j,k, on obtient une combinaison linéaire de i,j,k
où les coefficients sont des déterminants mineurs des coordonnées
de u et v.
Cette définition dépend fortement du choix de la base.

3) le produit vectoriel est défini par un théorème de représentation
de la forme linéaire det par un produit scalaire

est l'unique vecteur tel que
det

l'orientation de l'espace intervient dans cette définition du produit ,via
la forme "determinant"

4)le produit vectoriel est très utilisé en géométrie car lié à l'orientation
de l'espace:
si u,v est une base orthonormée plane, on peut la compléter
en une base orthonormée directe de l'espace par


5) en géométrie, on utilise ainsi:
on choisit une base orthonormée (i,j) dans le plan vectoriel
engendré par u et v, que l'on complète en une base orthonormée
directe i,j,k.
Alors, la composante sur k de est l'aire algébrique
du parallèlogramme construit sur u et v.

[mathelot]

re,

Le produit vectoriel vérifie, par définition,:



detdet

pour
8=3c-2b
pour
3=-5c+2a
pour
1=5b-3a

où (a,b,c) sont les coordonnées inconnues de