Equation second degré
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
HH.What?
- Membre Naturel
- Messages: 26
- Enregistré le: 06 Sep 2008, 11:16
-
 par HH.What? » 13 Sep 2008, 18:59
par HH.What? » 13 Sep 2008, 18:59

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 13 Sep 2008, 19:26
par nuage » 13 Sep 2008, 19:26
Salut,
sauf erreur de ma part, ton résultat est juste.
Je ne vois pas ce qui ne marche pas.
-
HH.What?
- Membre Naturel
- Messages: 26
- Enregistré le: 06 Sep 2008, 11:16
-
 par HH.What? » 13 Sep 2008, 21:05
par HH.What? » 13 Sep 2008, 21:05
Ok, c'est bon ca marche.
Je bloque sur 2 autres, pas évidentes..
(Z-1)=Z^2(Zbarre-1))
(Comment faire le signe barre svp?)
Puis l'autre


-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 13 Sep 2008, 21:26
par fatal_error » 13 Sep 2008, 21:26
Salut,
Pour le barre c'est \overline{a}=
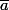
la vie est une fête

-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 13 Sep 2008, 23:02
par abcd22 » 13 Sep 2008, 23:02
Bonsoir,
HH.What? a écrit:(Z-1)=Z^2(Zbarre-1))
Ça se réécrit en
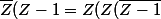))
, en prenant les modules on trouve le module de Z, ensuite passer aux arguments pour trouver une équation sur l'argument de Z (je rappelle la formule utile
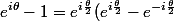 = ...)
)
Géométriquement, que représente |z - a| avec a et z des complexes ?
-
HH.What?
- Membre Naturel
- Messages: 26
- Enregistré le: 06 Sep 2008, 11:16
-
 par HH.What? » 14 Sep 2008, 10:57
par HH.What? » 14 Sep 2008, 10:57
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 14 Sep 2008, 11:35
par abcd22 » 14 Sep 2008, 11:35
Il n'y a (presque) aucun calcul à faire pour la deuxième, il suffit d'interpréter géométriquement l'équation.
Bon il faut trouver une droite donc peut-être que ton résultat est bon, je n'ai pas vérifié.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités