Ensembles et Applications

[Trevor]

Bonjour, je suis en Prépa MPSI et j'ai un exercice de mathématiques que je n'arrive pas à faire. Pourriez-vous m'aider s'il vous plaît ? Merci d'avance.
Voici l'énoncé de l'exercice :

Soit une application f : E -> F (E et F deux ensembles), on sait que f induit l'application f*, telle que f* : P(E) -> P(F), définie par : pour tout A inclus dans E, f*(A) = f[A].

Etude de quelques exemples : pour chacune des applications g suivantes, de P(E) à valeurs dans P(F), existe-t-il une application f : E -> F telle que g = f* ? Si oui, préciser celle-ci.

1) E est un ensemble non vide quelconque, X une partie non vide de E, F = E et g1 est l'application : A inclus dans E -> A réunion X.

2) E = F = N (N: ensemble des entiers naturels).
g2 : P(N) -> P(N)
A -> 2A = {2k|k appartenant à A}

3) E = F = N
g3 : P(N) -> P(N)
A -> {k appartenant à N|k+1 appartenant à A}

Voilà, c'est la partie de l'exercice que je ne parviens pas à faire, car je dois dire que je comprends pas. quelqu'un pourrait-il donc m'aider ?

[nuage]

Salut,
est l'ensemble des tels que
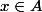
Pour le premier exercice, tu peux chercher (à partir de la définition) et tu auras la réponse.
Le deuxième me semble assez simple (application directe de la définition) peut-tu préciser ce qui te bloques ?
Le troisième comporte un petit piège.

[Trevor]

Tout d'abord, merci d'avoir répondu !
Ce qui me bloque, c'est que dans la question, je n'arrive pas à visualiser où se trouve une application, en fait je ne comprends pas comment trouver une application dans ce qui est donné, particulièrement dans la question 1.

Pour la question 2, par exemple, est-ce qu'il peut exister une application f2 telle que f2 : X -> 2X ? (et comment rédige-t-on une telle application ? Comme je viens de le faire, où bien faut-il se servir d'un ensemble déjà donné, etc... ?)

Par contre, je ne comprends pas à quoi correspond f*(ensemble vide) pour la question 1 ; pourrais-tu m'éclaircir s'il te plaît ?

Par contre, pour la question 3, je ne vois pas du tout (c'est encore du au fait que je n'arrive pas à comprendre comment en déduire une application, je pense).

Merci !

[nuage]

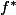
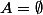
L'image par d'une partie A de E est la partie de F formée par les images des éléments de A. Si il n'y a pas d'éléments dans A () que peut-il y avoir dans ?

Pour la question 2 tu donnes la réponse :
et

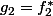
Pour la trois : si alors et réciproquement.
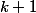
Comment passe t-on de à ?

[Trevor]

Grâce à toi, je crois que ça commence à s'éclaircir, dans cette zone brumeuse et sombre qu'est mon esprit ! Merci !

Donc, j'essaye :

1) Ben s'il n'y a pas d'éléments dans f, alors il ne doit pas pouvoir y en avoir dans f*(A). Et de ça, que peut-on en déduire ? Qu'il n'existe pas de f1 ? Et si tel est le cas, uniquement le fait de dire ce qu'on a dit, cela permet de justifier ? Ou pas ?

2) Bon ben t'as déjà donné la réponse. :we:

3) Pour passer de k+1 à k, on enlève 1 (trop fort !). Mais où est le piège ? Je dois dire que je ne vois pas trop ce qu'il faut faire, désolé... :triste:

[nuage]

Pour le 1) or

Pour le 3) on doit penser à la fonction. je te laisse chercher ce qui ne va pas...

[Trevor]

3) Si k = 0 cela ne peut pas fonctionner, car on se retrouverait avec -1, et on sait que A inclus dans E inclus dans N (entiers naturels). Donc il n'existe pas d'application f3. C'est ça ? (ou bien suis-je encore à côté de la plaque ? :briques: )

[nuage]

C'est ça :zen: :zen:

[Trevor]

Youhou ! Merci beaucoup pour ton aide précieuse ! :zen: