Besoin de vérification!

[nivéa]

soit, la fonction

a. trouver les points critiques de la fonction f



Résolvons ce système:



Soit


Comme est une fonction différente de 0, alors
le système devient:



Premier cas y#0
, on trouve que
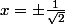
On remplace le résultat de (1) dans la (2) et on trouve que

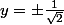Deuxième cas y=0
x=y=0

Les points critiques sont:

[nuage]

Salut,
je ne vois rien à ajouter. C'est juste.

[Cauchy3]

Premier cas y#0
, on trouve que
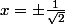
On remplace le résultat de (1) dans la (2) et on trouve que

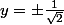
Tout est bon sauf pour bien rédiger il fallait écrir :
Premier cas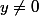
(1) implique que , on trouve que
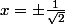
On remplace le résultat dans la (2) et on trouve que

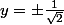
[leon1789]

Un remarque d'ordre "rédactionnel" juste en passant :

je préfère lire



Exactement comme on dit que f'(x)=x²+1 , et non f' = x²+1 qui ne veut a priori rien dire.