bonjour,
il s'agit là d'un sujet de maths de 1829(de l'ENS)!
je dois exposer une méthode permettant, sur une équation de degré quelconque, de donner une limite supérieure des racines positives.
j'ai essayé de chercher en partant des relations entre les racines d'un polynôme et ses coefficients mais cela ne donne rien....
Si quelqu'un à une petite idée, je suis preneur..
merci,
zoé
équation de degré quelconque
7 messages
- Page 1 sur 1
l'énoncé est :
Exposer, sur une équation de degré quelconque,le moyen d'obtenir :
1- une limite superieure des racines positives.
si X1,...,XP sont les racines, oui je crois que tu as raison :
regarde ce que j'ai trouvé (malheureusement je ne comprend pas tout)
http://www.numdam.org/numdam-bin/fitem?id=AMPA_1829-1830__20__297_0
Exposer, sur une équation de degré quelconque,le moyen d'obtenir :
1- une limite superieure des racines positives.
si X1,...,XP sont les racines, oui je crois que tu as raison :
regarde ce que j'ai trouvé (malheureusement je ne comprend pas tout)
http://www.numdam.org/numdam-bin/fitem?id=AMPA_1829-1830__20__297_0
bjr,
une idée (bovine) c'est qu'un polynome est équivalent à son terme
de plus haut degré quand x tend vers
si=a_n x^n +a_{n-1}x^{n-1}+ ..+a_{0})
|=|a_n||x|^n \, |1 +\frac{a_{n-1}}{a_{n} x}+..+\frac{a_0}{a_n x^n}|)
comme
| \geq |a_n||x|^n |1 -|\frac{a_{n-1}}{a_{n} x}+..+\frac{a_0}{a_n x^n}||)
Dès que x est assez grand ,la différence est supérieure à car elle tend vers 1 et donc P(x) ne s'annule plus.
car elle tend vers 1 et donc P(x) ne s'annule plus.
or
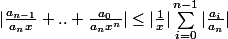 si
si 
d'où si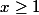 et
et 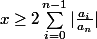
 \neq 0)
donc en valeurs absolues, les racines sont inférieures à la quantité
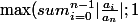)
une idée (bovine) c'est qu'un polynome est équivalent à son terme
de plus haut degré quand x tend vers
si
comme
Dès que x est assez grand ,la différence est supérieure à
or
d'où si
donc en valeurs absolues, les racines sont inférieures à la quantité
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
