Problème d'intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 05 Sep 2008, 15:48
par nivéa » 05 Sep 2008, 15:48

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 05 Sep 2008, 15:58
par nuage » 05 Sep 2008, 15:58
Salut,
J'iamgine que tu veux calculer
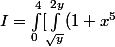\, {\mathrm d} x]{\mathrm d} y)
Je ne vois pas bien pourquoi changer l'ordre d'intégration.
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 05 Sep 2008, 16:00
par Cauchy3 » 05 Sep 2008, 16:00
Sauf erreur de calcul, tout est bon, faites un petit schéma si vous ne voyez pas.
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 05 Sep 2008, 16:01
par Cauchy3 » 05 Sep 2008, 16:01
nuage a écrit:Salut,
J'iamgine que tu veux calculer
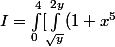\, {\mathrm d} x]{\mathrm d} y)
Je ne vois pas bien pourquoi changer l'ordre d'intégration.
je pense que c'est le début des exercices sur les intégrales doubles, pour une maîtrise de calcul.

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 05 Sep 2008, 16:07
par nuage » 05 Sep 2008, 16:07
Salut,
Cauchy3 a écrit:je pense que c'est le début des exercices sur les intégrales doubles, pour une maîtrise de calcul.
Tu as certainement raison, je n'y avais pas pensé

-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 05 Sep 2008, 16:09
par nivéa » 05 Sep 2008, 16:09
donc, on obtient (après avoir changé l'ordre d'intégration):
\, \mathrm dy]dx)
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 05 Sep 2008, 16:13
par Cauchy3 » 05 Sep 2008, 16:13
Oui, encore une fois si je me suis pas trompé dans les calculs.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 05 Sep 2008, 16:21
par nivéa » 05 Sep 2008, 16:21
je suis désolée j'ai oublié une puissance 2008, je l'ai modifié dans mon 1er message.
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 05 Sep 2008, 16:28
par Cauchy3 » 05 Sep 2008, 16:28
nivéa a écrit:je suis désolée j'ai oublié une puissance 2008, je l'ai modifié dans mon 1er message.
Pour le Latex il faut mettre 2008 entre
accolades pour apparaître comme puissance.
Mais 2008 ou autre chose cela ne change rien, les domaine est à un certain moment indépendant de la fonction à intégrer.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 05 Sep 2008, 17:10
par nivéa » 05 Sep 2008, 17:10
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 05 Sep 2008, 17:20
par Cauchy3 » 05 Sep 2008, 17:20
nivéa a écrit:je me lance:
^(2008)\, \mathrm dy)
^(2008)])
au borne
)
Oui c'est bien ça :
^{2008}]_{0}^{x^2^}=)
(j'ai rectifié il fallait écrire 2008 entre deux accolades)
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 05 Sep 2008, 17:33
par nivéa » 05 Sep 2008, 17:33
Cauchy3 a écrit:Oui c'est bien ça :
^{2008}]_{0}^{x^2^}=)
(j'ai rectifié il fallait écrire 2008 entre deux accolades)
alors,
^{2008}]_{0}^{x^2^}= \frac {x^4}{2}(1+x^5)^{2008})
!!!
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 05 Sep 2008, 17:38
par Cauchy3 » 05 Sep 2008, 17:38
nivéa a écrit:alors,
^{2008}]_{0}^{x^2^}= \frac {x^4}{2}(1+x^5)^{2008})
!!!
Oui, très bien fait, reste à intégrer par rapport à x.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 05 Sep 2008, 17:42
par nivéa » 05 Sep 2008, 17:42
c'est là ou ça se complique!!
je me rappel d'un truc mais, je suis pas sur: il faut faire la linéarisation, nan!!!
-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 05 Sep 2008, 17:47
par Cauchy3 » 05 Sep 2008, 17:47
nivéa a écrit:c'est là ou ça se complique!!
je me rappel d'un truc mais, je suis pas sur: il faut faire la linéarisation, nan!!!
Linéarisation c'est pour les fonctions trigonométriques pas pour les polynômes,
Question préliminaire :
Comment vous calculez cette intégrale :
^{10} dx)
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 05 Sep 2008, 18:44
par nivéa » 05 Sep 2008, 18:44
alors quand j'intègre :

-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 05 Sep 2008, 19:00
par Cauchy3 » 05 Sep 2008, 19:00
nivéa a écrit:alors quand j'intègre :

Si on pose

; il sagit alors de calculer

-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 05 Sep 2008, 21:28
par nivéa » 05 Sep 2008, 21:28
si on intègre 1+x^5 cela ne devient pas:

-
Cauchy3
- Membre Naturel
- Messages: 49
- Enregistré le: 23 Aoû 2008, 21:57
-
 par Cauchy3 » 05 Sep 2008, 21:35
par Cauchy3 » 05 Sep 2008, 21:35
nivéa a écrit:si on intègre 1+x^5 cela ne devient pas:

Oui ça c'est vrai mais vous avez oublié que

est élevé à une puissance :

Pour ne pas tarder sur cette question calculatoire, je vous rappelle que :

avec

Dans l'integrale qu'on souhaite calculer

et n=2008, la question qui se pose : a-t-on u' à coté de

-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 06 Sep 2008, 16:26
par nivéa » 06 Sep 2008, 16:26
comment intégrer la fonction suivante:
^{2008}\, \mathrm dx)
une piste!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités


