Racine d'un polynome
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
neuneu
- Membre Relatif
- Messages: 290
- Enregistré le: 28 Sep 2006, 18:14
-
 par neuneu » 03 Sep 2008, 20:08
par neuneu » 03 Sep 2008, 20:08
Bonsoir , je suis bloqué sur cet exercice.Pourriez vous m'aider s'il vous plait.
Soit
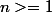
=x^n+x^{n-1}+..+x-1)
Montrer que

admet une unique racine positive

.
Montrer que
<0)
.
En déduire le sens de variation de (

) et montrer qu'elle converge.
Je ne vois pas comment commencer
Merci

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 03 Sep 2008, 20:12
par leon1789 » 03 Sep 2008, 20:12
Cet exercice a été abordé il n'y a pas longtemps, mais je ne le trouve plus. Si quelqu'un peut le trouver... :id:
-
mathelot
 par mathelot » 03 Sep 2008, 20:13
par mathelot » 03 Sep 2008, 20:13
Bjr,
tu peux par exemple:
- calculer
)
et
)
calculer
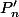
et son signe sur [0,1]
calculer
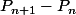
ou bien
marcher pieds nus sous la pluie :zen:
-
neuneu
- Membre Relatif
- Messages: 290
- Enregistré le: 28 Sep 2006, 18:14
-
 par neuneu » 03 Sep 2008, 20:29
par neuneu » 03 Sep 2008, 20:29
J'ai
=-1)
et
=n-1)
=nx^{n-1}+(n-1)x^{n-2}+...+x)
et sur [0,1]c'est positif car on va faire une somme de nombre positif
-
neuneu
- Membre Relatif
- Messages: 290
- Enregistré le: 28 Sep 2006, 18:14
-
 par neuneu » 03 Sep 2008, 20:38
par neuneu » 03 Sep 2008, 20:38
Donc

est croissante de [0,1] sur [-1,n-1]
donc d'après le théorème des valeurs intermédiaires , il existe un

appartenant à ]0,1[ tel que
=0)
.
Mais là on ne travaille que sur [0,1], comment fait on pour travailler sur R et donc montrer que ce

est unique ?
Merci
-
mathelot
 par mathelot » 03 Sep 2008, 20:47
par mathelot » 03 Sep 2008, 20:47
neuneu a écrit:comment fait on pour travailler sur R et donc montrer que ce

est unique ?
on travaille sur
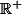
donc il y a une unique racine positive qui appartient à ]0,1[.
on peut essayer une relation entre
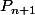
et

-
neuneu
- Membre Relatif
- Messages: 290
- Enregistré le: 28 Sep 2006, 18:14
-
 par neuneu » 03 Sep 2008, 20:51
par neuneu » 03 Sep 2008, 20:51
Comment savez vous qu'on travaille sur R+ s'il vous plait?
merci
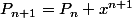
-
mathelot
 par mathelot » 03 Sep 2008, 20:57
par mathelot » 03 Sep 2008, 20:57
neuneu a écrit:Montrer que

admet une unique racine
positive
:doh: :doh:
-
neuneu
- Membre Relatif
- Messages: 290
- Enregistré le: 28 Sep 2006, 18:14
-
 par neuneu » 03 Sep 2008, 21:00
par neuneu » 03 Sep 2008, 21:00
Oui pardon je ne voyais pas !
donc en fait il faut que je montre que sur [1,+inf[ il n'y a pas de racine ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 03 Sep 2008, 21:14
par leon1789 » 03 Sep 2008, 21:14
neuneu a écrit:donc en fait il faut que je montre que sur [1,+inf[ il n'y a pas de racine ?
oui, mais sur
]1,+inf[ (because x-1 ...)
Et c'est assez simple, non ?
-
mathelot
 par mathelot » 03 Sep 2008, 21:27
par mathelot » 03 Sep 2008, 21:27
neuneu a écrit:Comment savez vous qu'on travaille sur R+ s'il vous plait?
merci
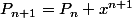
avec cette relation, c presque fini. remplacer x par
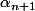
-
neuneu
- Membre Relatif
- Messages: 290
- Enregistré le: 28 Sep 2006, 18:14
-
 par neuneu » 05 Sep 2008, 11:35
par neuneu » 05 Sep 2008, 11:35
Bonjour veuillez m'excuser de ne pas être revenu avant.
Merci pour votre aide mais je dois être à côté de tout car je ne comprends pas grand chose...
Pourquoi est ce que c'est facile de montrer que sur ]1;+inf[ il n'y a pas de racines s'il vous plait?
Merci
=P_n(a_{n+1})+(a_{n+1})^{n+1})
Merci de votre et désolé encore de ne pas avoir répondu avant

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 05 Sep 2008, 13:27
par nuage » 05 Sep 2008, 13:27
neuneu a écrit:[...]
Pourquoi est ce que c'est facile de montrer que sur ]1;+inf[ il n'y a pas de racines s'il vous plait?
[...]
Parce que si
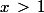
alors

et donc
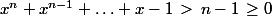
pour

entier strictement positif.
-
digardel
- Membre Naturel
- Messages: 84
- Enregistré le: 26 Aoû 2008, 15:36
-
 par digardel » 05 Sep 2008, 13:57
par digardel » 05 Sep 2008, 13:57
Pas la peine de calculer de dérivés là.toutes les fonctions qui internviennent dans ta somme sont des puissances donc croissantes sur r +
La fonction est croissante sur IR +
Elle est de plus continue donc elle réalise une bijection de R+ sur son image avec f(o) = -1 et f (1) = n -1 c est pas tres dur de conclure
-
digardel
- Membre Naturel
- Messages: 84
- Enregistré le: 26 Aoû 2008, 15:36
-
 par digardel » 05 Sep 2008, 14:07
par digardel » 05 Sep 2008, 14:07
aprés tu as pn(an)=0 et Pn(an+1) négatif et de plus Pn est bijective croissante ,pense à la fonction réciproque et l exo est fini
-
neuneu
- Membre Relatif
- Messages: 290
- Enregistré le: 28 Sep 2006, 18:14
-
 par neuneu » 05 Sep 2008, 15:00
par neuneu » 05 Sep 2008, 15:00
Bonjour merci de m'aider!
Alors merci nuage et digardel j'ai compris pourquoi sur ]1;+inf[ il n'y a pas de racine.C'était assez évident mais je n'avais pas vu , désolé.
Mais digardel pourquoi
)
est négatif s'il te plait.C'est quoi

?
Parce que si j'ai
<0)
alors forcément

<

puisque

est croissante et
=0)
Merci

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 05 Sep 2008, 15:37
par nuage » 05 Sep 2008, 15:37
Question surprenante :

est, par définition, la racine réelle de
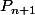
.
On a donc :
 =0)
or
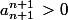
donc ...
-
neuneu
- Membre Relatif
- Messages: 290
- Enregistré le: 28 Sep 2006, 18:14
-
 par neuneu » 05 Sep 2008, 17:35
par neuneu » 05 Sep 2008, 17:35
Merci nuage !! je comprends beaucoup mieux le problème maintenant. Je n'arrivais pas à comprendre entre les

et les

mais maintenant j'ai compris tous les messages précédents!
Je comprends vos différentes réactions face à mon incompréhension!
Donc j'ai bien maintenant que
)
0 car 0 n'est racine d'aucun

quelque soit n.
On a donc une suite décroissante et minorée donc elle converge.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 05 Sep 2008, 18:04
par leon1789 » 05 Sep 2008, 18:04
neuneu a écrit:)
0 car 0 n'est racine d'aucun

quelque soit n.
On a donc une suite décroissante et minorée donc elle converge.
Pour moi, c'est ok, bien que je pense qu'il y a un peu plus simple pour démontrer que la suite
_n)
est décroissante.
Au fait, peux-tu dire vers quoi tend la suite
_n)
?
-
neuneu
- Membre Relatif
- Messages: 290
- Enregistré le: 28 Sep 2006, 18:14
-
 par neuneu » 05 Sep 2008, 18:12
par neuneu » 05 Sep 2008, 18:12
j'aurais envie de dire qu'elle tend vers 0 mais je ne sais pas comment le démontrer
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités