Calcul
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Loireni
- Membre Naturel
- Messages: 13
- Enregistré le: 04 Sep 2008, 16:45
-
 par Loireni » 04 Sep 2008, 16:48
par Loireni » 04 Sep 2008, 16:48
Pouvez m'aider a réaliser :
3
sur
Racine de 2 + Racine de 3
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 04 Sep 2008, 16:53
par Clembou » 04 Sep 2008, 16:53
Loireni a écrit:Pouvez m'aider a réaliser :
3
sur
Racine de 2 + Racine de 3
En LaTex : \frac{3}{\sqrt{2}+\sqrt{3}}
Ce qui nous donne :

-
phryte
- Membre Irrationnel
- Messages: 1406
- Enregistré le: 05 Juil 2008, 17:09
-
 par phryte » 04 Sep 2008, 16:53
par phryte » 04 Sep 2008, 16:53
Slt.
Tu multiplies haut et bas par la quantité conjuguée.
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 04 Sep 2008, 16:54
par le_fabien » 04 Sep 2008, 16:54
Bonsoir,
est ce

à transformer ?
-
Loireni
- Membre Naturel
- Messages: 13
- Enregistré le: 04 Sep 2008, 16:45
-
 par Loireni » 04 Sep 2008, 16:55
par Loireni » 04 Sep 2008, 16:55
Oui c'est bien sa :)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 04 Sep 2008, 17:00
par leon1789 » 04 Sep 2008, 17:00
phryte a écrit:Slt.
Tu multiplies haut et bas par la quantité conjuguée.
Oui, mais il y a ici 2 racines carrées, donc 2² = 4 conjugués
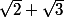
,

,

,

-
phryte
- Membre Irrationnel
- Messages: 1406
- Enregistré le: 05 Juil 2008, 17:09
-
 par phryte » 04 Sep 2008, 17:14
par phryte » 04 Sep 2008, 17:14
Oui, mais il y a ici 2 racines carrées, donc 2² = 4 conjugués , , ,
On prend :


-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 04 Sep 2008, 17:16
par leon1789 » 04 Sep 2008, 17:16
phryte a écrit:On prend :

non, on les prend tous pour faire disparaître toutes les racines du dénominateur.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 04 Sep 2008, 17:20
par Timothé Lefebvre » 04 Sep 2008, 17:20
Tu dois trouver un résultat non fractionnaire. En gros ton but est de supprimer la fraction ; tu vois comment faire ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 04 Sep 2008, 17:29
par leon1789 » 04 Sep 2008, 17:29
Timothé Lefebvre a écrit:Tu dois trouver un résultat non fractionnaire
Tu es certain qu'à la fin c'est "non fractionnaire" ?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 04 Sep 2008, 17:31
par Timothé Lefebvre » 04 Sep 2008, 17:31
Oui, le résultat de

n'est pas une fraction !

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 04 Sep 2008, 17:35
par leon1789 » 04 Sep 2008, 17:35
Timothé Lefebvre a écrit:Oui, le résultat de

n'est pas une fraction !
après calcul... c'est exact ! :id:
(ne pas prendre ce cas particulier pour une généralité)
EDIT : Ok,

conduit à
^2)
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 04 Sep 2008, 17:39
par Timothé Lefebvre » 04 Sep 2008, 17:39
leon1789 a écrit:EDIT : Ok,

conduit à
^2)
Tu es sûr ? ...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 04 Sep 2008, 17:45
par leon1789 » 04 Sep 2008, 17:45
Timothé Lefebvre a écrit:Tu es sûr ? ...
:ptdr: ouais :zen: (je parle du dénominateur)

aussi bien sûr.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 04 Sep 2008, 17:46
par Timothé Lefebvre » 04 Sep 2008, 17:46
leon1789 a écrit::ptdr: ouais :zen:

aussi bien sûr.
Euh ... Je comprends pas !

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 04 Sep 2008, 17:52
par leon1789 » 04 Sep 2008, 17:52
Timothé Lefebvre a écrit:Euh ... Je comprends pas !
ben
^2})
Ici, on a=2 et b=3 , d'où un dénominateur = (2-3)² = 1
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 04 Sep 2008, 17:53
par Timothé Lefebvre » 04 Sep 2008, 17:53
Ah ouky ! Moi je voyais ton égalité sous l'oeil des identités remarquables, c'est pour ça ...
-
Loireni
- Membre Naturel
- Messages: 13
- Enregistré le: 04 Sep 2008, 16:45
-
 par Loireni » 04 Sep 2008, 17:55
par Loireni » 04 Sep 2008, 17:55
Je comprend pas non plus ... :s
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 04 Sep 2008, 18:01
par Euler911 » 04 Sep 2008, 18:01
Bonjour,
\,\left(\sqrt{a}-\sqrt{b}\right)\, \left(\sqrt{b}-\sqrt{a}\right)\,\left(\sqrt{b}+\sqrt{a}\right)=(a-b)^2)
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 04 Sep 2008, 18:01
par Timothé Lefebvre » 04 Sep 2008, 18:01
Si en fait c'est bon, c'est juste que le message de leon1789 que j'ai relevé portait un peu à confusion.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
