Doraki a écrit:Ben c'est faux c'est plutot
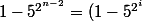(1 + 5^{2^i} + 5^{2.2^i} + 5^{3.2^i} + \cdots + 5^{2^{n-2}-2^i}))
Mais je sais pas où leon veut en venir avec cette factorisation
On veut démontrer que i=n-2 (ainsi l'ordre de 5 sera
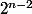
) , autrement dit que le facteur
)
vaut 1.
Maintenant, la fin de l'exo est toute proche : :++:
On sait que
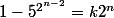
avec k
impair (remarquer que jusqu'ici, on ne s'est jamais servi de la parité de k ! C'est donc le moment ou jamais :we: )
On sait aussi que
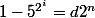
avec
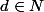
(car
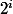
est l'ordre multiplicatif de 5 modulo

)
On reporte tout ça dans la factorisation :
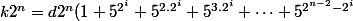)
ou encore
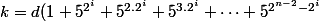)
en simplifiant par

avec
k impair, ce qui implique que d et
)
sont également impairs.
Trois petites questions pour terminer :
Combien il y a-t-il de termes dans la somme
)
?

(indication :
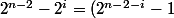2^i)
)
Quelle est la parité de chacun des termes de cette somme ?
Pour quelle valeur de i la somme est-elle impaire ?
Voilà, finished :zen:
, c'est
, pas 2 que je sache ! On sait que
mais on ne sait rien sur
...
?? :marteau:
